You may also like

problem icon

Achi

This game for two players comes from Ghana. However, stones that were marked for this game in the third century AD have been found near Hadrian's Wall in Northern England.

problem icon

Yih or Luk Tsut K'i or Three Men's Morris

Some puzzles requiring no knowledge of knot theory, just a careful inspection of the patterns. A glimpse of the classification of knots and a little about prime knots, crossing numbers and knot arithmetic.

problem icon

Lambs and Tigers

Investigations based on an Indian game.

Snail Trails

Stage: 3 Challenge Level: Challenge Level:1

This is a game for two players. You will need some small-square grid paper, a die and two felt-tip pens or highlighters.

  1. Mark a starting point and a target square.
  2. Players take turns to roll the die, then move that number of squares in a straight line.
  3. Move only vertically (up/down) or horizontally (across), never diagonally.
  4. You can cross over the other player's trails. You can trace over the top of the other player's trails.
  5. You can cross over a single trail of your own, but can never cross a pair of your trails (side-by-side) or trace over your own trail.
  6. To win, you must roll the exact number needed to finish in the target square. You can never pass through the target square.
  7. The game ends when a player ends his/her trail in the target square, OR when a player cannot move without breaking any of the rules.
Grid

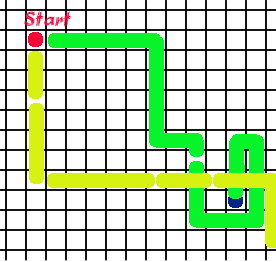
Does it matter where the target is put? Is there a good strategy for winning? If you could choose your own numbers, what would be the shortest possible trail?

The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice. More information on many of our other activities can be found here.
Copyright © 1997 - 2012. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.