 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Totality



- Problem
- Student Solutions
- Teachers' Resources
Totality
This is a game for two players.
You will need a copy of the game board and a counter.
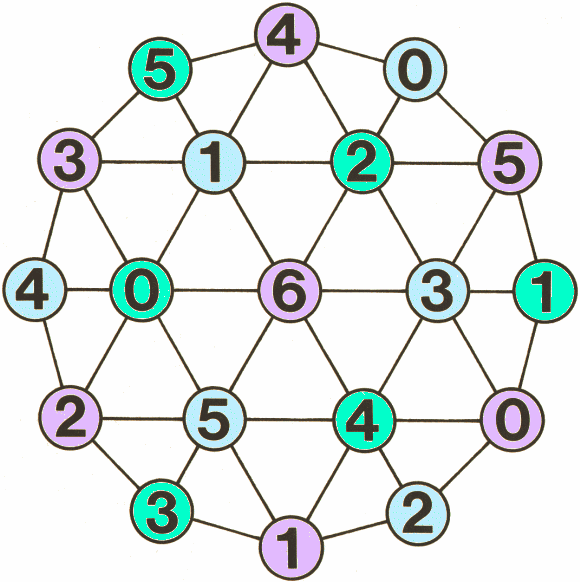
Watch the video below (which has not got any sound). It shows two people playing the game.
Can you work out how to play the game?
What do you think the rules might be?
If you are unable to view the video, the rules of the game are hidden below.
Slide the shared counter across several adjacent numbers, adding them up as you go to make a 'running' total. Be the player to make the final slide so that the chosen target is reached exactly. Making the total go above the target loses you the game.
How to play:
1. Player 1 chooses a target to reach. This is the total both players try to make.
2. Player 2 places their counter on the game board over one of the numbers and says that number.
3. Player 1 moves the same counter in any direction along a line segment to a neighbouring number and announces the total of the two numbers.
4. Player 2 moves the same counter to cover a neighbouring number, adds on that number, and announces the 'running' total of the three numbers.
5. Players take it in turns to slide the counter to cover a neighbouring number and to add that number to the 'running' total.
6. Players must move when it is their turn.
7. No 'jumping' is allowed.
Have a go at playing the game several times.
Can you find any good ways to win?
Why play this game?
Totality is a low threshold high ceiling game which offers the opportunity for children to become more fluent with number bonds and addition. At a higher level, learners can begin to think strategically by considering several moves in advance.Possible approach
In the video below, you can see the game being played in silence. Show this to the group, simply saying that you'd like them to watch carefully to see whether they can work out the rules of the game.Give them chance to talk in pairs about the possible rules. Emphasise that they may not be completely sure and that is alright. They may even have some questions to seek clarity. After a suitable length of time, show the video again so that learners can check their initial thoughts.
Then bring everyone together and reveal the rules of the game on the screen by clicking the 'Show' button in the main problem page. Try to keep silent yourself (other than reading out the rules) and then give learners chance to talk to their partner again.
Next you can show them the following video, which does have sound, and so explains how to play:
Facilitate a whole group discussion in order to agree on the rules, and once everyone is clear, give pairs a copy of the game board each and a counter. Allow them time to play the game several times without saying much more yourself. It is important that learners are able to 'get into' the game before being expected to analyse it in detail.
You could then invite the group to begin to think about good ways of winning (if they haven't done so already). At this point, you could put them in groups of four so that they play two against two. This gives them the opportunity to discuss strategy with their partner.
The session could culminate in the creation of a list of 'top tips' for anyone playing this game and wanting to win.
See also the possible adaptations sent in from one class.
Key questions
What do you need to make your target?Where could you go next?
What might your opponent do then?
Possible adaptations
Tokyo class at Manorfield Primary School, London, came up with some wonderful adaptations to the game.
Renah and Sami played so that you could choose any calculation. They removed the "bust" rule which meant that players could be mean and multiply the number far beyond the target number! They then thought about using more than one move a turn. They could then use brackets to change the order of operations and come up with more possibilities.
Rumaysa and Chloe introduced a minimum target number in order to make the games last longer.
Adil and Ahsanur added the choice of moving 1,2 or 3 times. They also got to choose which calculation to use. They found it annoying when someone was able to multiply by 0 and had to start again!
Samah and Khadija took it in turns to reach the target number with the fewest moves. They noticed the person that went second had an advantage.
Sameeha and Anaum made a decimal number version of the game. They turned the numbers into tenths. They then could change their target numbers into decimals.
Humairah and Aayana changed the rules so that any even number on the board you have to subtract and odd numbers you add. This became annoying when you were close to a number but an even number away, so then you would have to subtract.
Alex and Faisal added digits up to 9 on the board and made the playing board larger. This made it easier to get bigger numbers quicker.
Possible extension
- What is the shortest 'string' of numbers that adds to their chosen total?
- How many different 'strings' of numbers that add to their chosen total can they find?
- Could they design a different grid to make the game harder/easier? (Here are blank boards which may be useful: Word document, pdf.)
- What if the grid contained decimal numbers/fractions?
You could introduce the game Play to 37 as a follow-on to this one.
Martin Shaw who teaches at Seal Primary Academy in Selsey suggested the following:
- Play the game cooperatively i.e. both players work together to try to reach 20.
- Start at 20 and subtract the numbers on the grid to try to get to 0.
Possible support
You could put some children together in pairs straight away so that they have chance to talk to someone else as they play the game.