 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Graphing Number Patterns



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Graphing Number Patterns
The class were making number patterns and then making graphs of them.
Several children had plotted graphs of the "times tables". They made good-looking straight lines.
Tom had started on the six times table but had then decided to do something more interesting. He had made the triangular numbers with counters last year. That was a better idea, he thought.
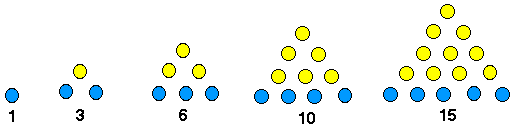
So he started to put them on the same graph paper as the unfinished six times table.

"It's not a very good straight line," he remarked to Andy who was sitting next to him.
"I think it's going to cross the six times line," answered Tom, "But you'll have to make a lot more of both of them. I'm going to try square numbers, I bet the tables one will cross that!"
Does the graph of the triangular numbers cross that of the six times table?
And if it does, where?
Does the graph of square numbers cross those of the times tables?
And if it does, where?