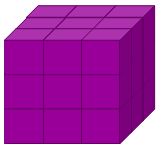
A $3 \times 3 \times 3$ cube may be reduced to unit cubes ($1 \times1 \times1$ cubes) in six saw cuts if you go straight at it.

If after every cut you can rearrange the pieces before cutting straight through, can you do it in fewer? Answer the same question with a $4 \times 4 \times 4$ cube:

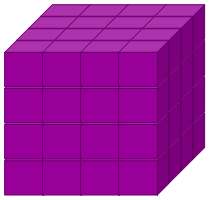
What about a cube of any size (an $n \times n \times n$ cube)?

This problem has been adapted from the book "Sums for Smart Kids" by Laurie Buxton, published by BEAM Education. This book is out of print but can still be found on Amazon.