 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Cubes Within Cubes



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Cubes Within Cubes
We had interlocking cubes (all the same size) in ten different colours, up to 1000 of each colour. We started with one yellow cube. This was covered all over with a single layer of red cubes:
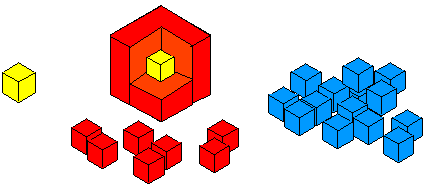
This was then covered with a layer of blue cubes.
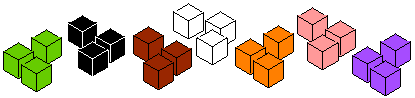
Then came a layer of green, followed by black, brown, white, orange, pink and purple for as long as there were enough cubes of that colour to cover the layer that came before.
The unused cubes were put away.
The many-layered cube was then broken up and each colour made into cubes. These were just of the one colour and the largest cubes possible made.
For example, the red layer made three 2x2x2 cubes with two 1x1x1 cubes left over, whereas the larger layers made much larger cubes as well as smaller ones.
What colour was the largest cube that was made?
Which colour made into cubes had no 1x1x1 cubes?
Which colour was made into the most cubes including the 1x1x1 cubes?
Why do this problem?
This is a tough problem, ideal for learners who relish the challenge of working with large and difficult numbers. However, using interlocking cubes to create models of the situation will help children form mental images of cube numbers.Possible approach
It will be necessary to have a large supply of cubes available for this activity, although allow pupils to decide for themselves whether they make use of them.You could start by describing just a single yellow cube covered in a single layer of red cubes. Ask learners about the number of red cubes that would be needed and invite them to think on their own, then chat with a partner before sharing ideas. You may want to have a model already made to show the group after they have had chance to decide on the number. Pose a few other questions like this, perhaps asking the group to imagine a few layers, one at a time.
Then you can pose the question itself. You may find it useful to print off and hand out copies of this sheet which contains the problem.
It may be appropriate to ask pairs or small groups to work together on the challenge and then invite them to create a poster outlining how they approached the task. These could be displayed and time given in the plenary for all pupils to view them.
Key questions
Have you found out how many cubes are needed to cover the single cube?Have you remembered that there are only "up to 1000 of each colour"?
What is the cube root of 1000? How does this help you?
What size cubes are possible if the maximum number of cubes in one colour is 1000?