Copyright © University of Cambridge. All rights reserved.
'Cubes Within Cubes' printed from https://nrich.maths.org/
Show menu
We had interlocking cubes (all the same size) in ten different colours, up to 1000 of each colour. We started with one yellow cube. This was covered all over with a single layer of red cubes:
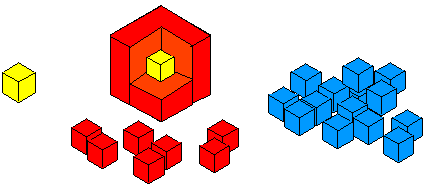
This was then covered with a layer of blue cubes.
Then came a layer of green, followed by black, brown, white, orange, pink and purple for as long as there were enough cubes of that colour to cover the layer that came before.
The unused cubes were put away.
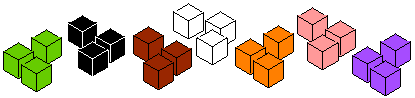
The many-layered cube was then broken up and each colour made into cubes. These were just of the one colour and the largest cubes possible made.
For example, the red layer made three 2x2x2 cubes with two 1x1x1 cubes left over, whereas the larger layers made much larger cubes as well as smaller ones.
What colour was the largest cube that was made?
Which colour made into cubes had no 1x1x1 cubes?
Which colour was made into the most cubes including the 1x1x1 cubes?