Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Three Cubed
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Three Cubed
Can you make a $3\times 3$ cube with these shapes made from small cubes?
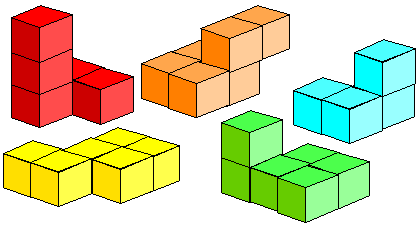
You can record your answer as either pictures or as a net of the cube.
Why do this problem?
This problem is one which can help learners to relate 2-D representations and 3-D shapes. It is definitely one which requires making the shapes practically from interlocking cubes such as "multilink" using the 2-D drawings and then recording on squared paper (preferably in colour).Key questions
Which shape are you making now?
How can those two shapes fit together?
Which side of the cube are you recording now?
Which side of the cube comes next to that side?