 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Square Corners



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Well done to everybody who solved this problem! We had lots of solutions telling us that 10 is the maximum number of counters you can place on the grid without making a square. The following solutions came from children who explained their reasoning particularly clearly.
Dhruv, who is homeschooled in the UK, sent in this picture showing one possible solution:
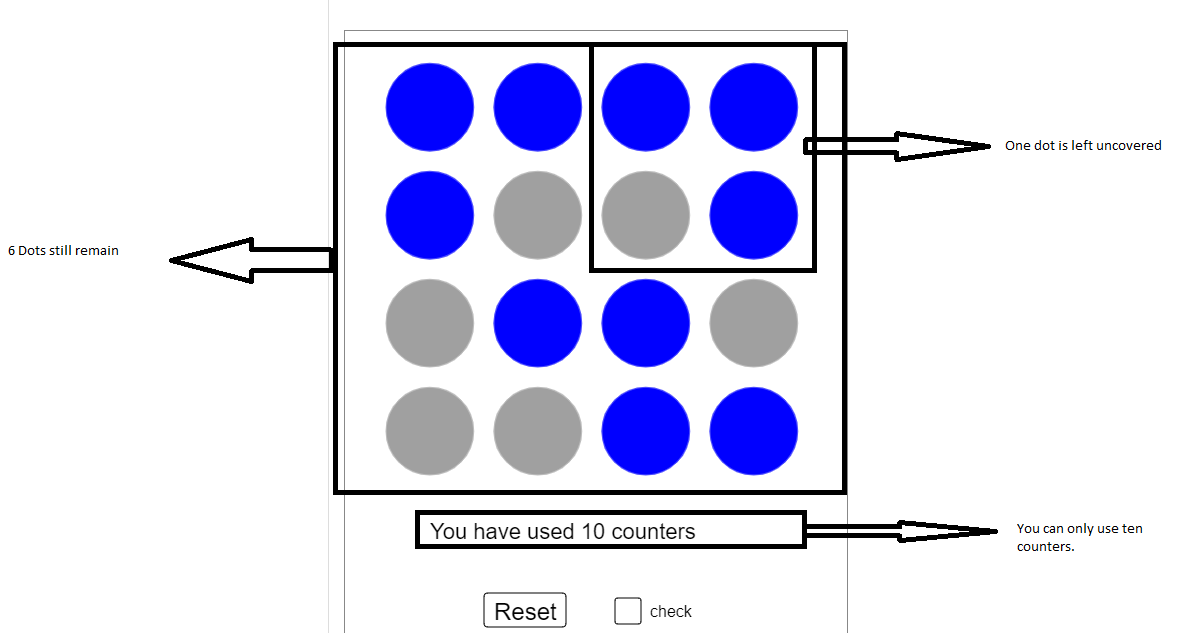
Thank you Dhruv!
Saanvi from Newcastle under Lyme Prep School in England said:
I started by filling in all of the circles and checking how many squares there were and, of course, there were lots. I then chose a point that I think has a large amount of squares coming from it and unselected it. I then repeated the process again and again to find an answer. I found a way of using 9 circles, but then I thought that it might be possible to have more points used, so I tried again and found it that I could use 10 points. I don’t think that it is possible to use 11 because, just to check my answer, I checked every combination of 11 circles and every time found that there were some squares made.
Well done Saanvi - it must have taken you a while to check every combination of 11 circles!
K from Crossflatts in the UK had a similar strategy. Have a look at K's full solution to see the step-by-step process of how they chose which counters to remove at each point. Thank you for sending in this very clear explanation of your thinking, K - we've kept everything you wrote but we've tweaked the format of your pictures to make it easier to read.
We also had some good explanations sent in from: Liam from Furness Academy in England; Milly from Drake Primary School in Thetford; Sachkeerat from Akal Academy Baru Sahib, Himachal Pradesh in India; Anna and Serenade from Sahuaro Elementary Gifted Learning Center in the USA; and Ci Hui Minh Ngoc from Kong Hwa School in Singapore. Thank you all for sending us your solutions.
Charlotte from Halstead Prep School in the UK tried this challenge on a variety of different sizes of grid, and she noticed an interesting pattern:
In a 2 x 2 square I can put three counters. In a 3 x 3 square I think I can put 6 counters. In a 4 x 4 I think 10 and in a 5 x 5 I could put 15. These are part of the triangular sequence and that stops you having squares.
Well done Charlotte, I think you're right - on those grids the answers will be triangular numbers each time. If the pattern continues, I wonder how many counters you could put on a 6 x 6 grid without making any squares? What about a 7 x 7 grid?
You may also like
Geoboards
This practical challenge invites you to investigate the different squares you can make on a square geoboard or pegboard.