Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Shopping Basket
Age 11 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
For three items whose prices add and multiply to £5.88
Erin from York House School in Canada used a method similar to Alison's first method:
First I put 1 as one of my numbers because any number multiplied by 1 equals that number. Next I tried a bunch of numbers after that without 1 just to see the answer. You can see this in the first 4 lines of my work:
(Note that Erin has written + between each number, but in the fourth line, she has worked out the product, rather than the sum. The sum is 5.88.)
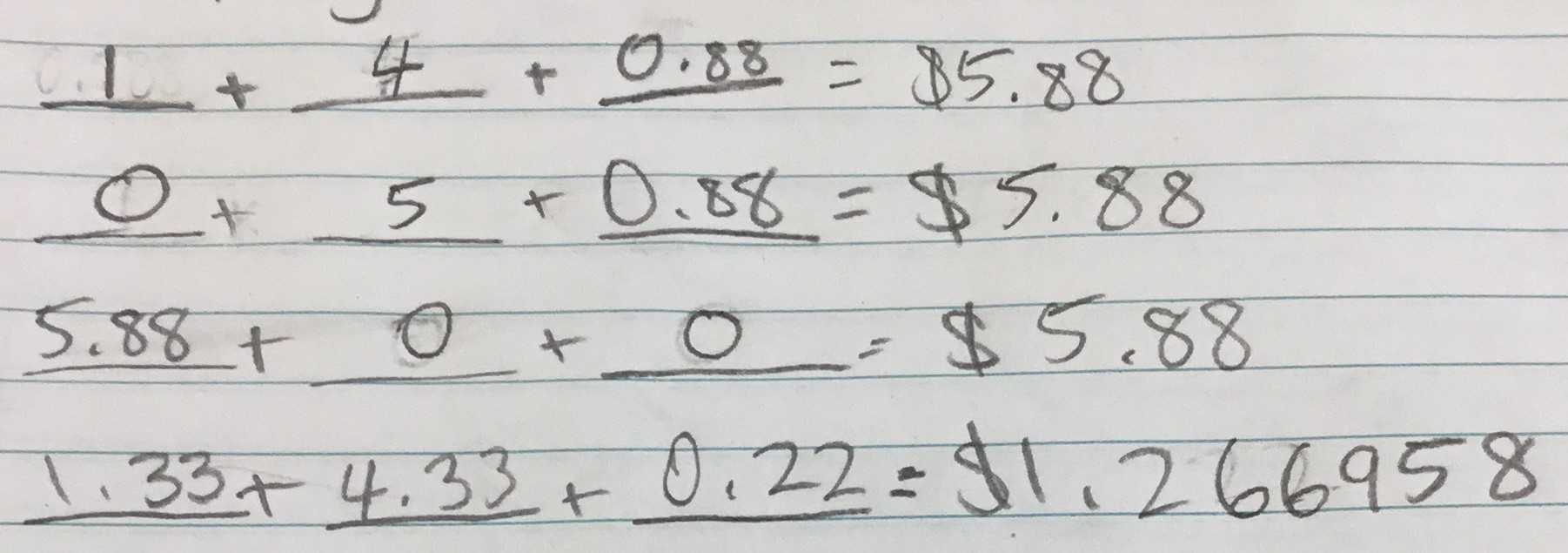
Then I realized that I was not making that much progress so I asked my teacher. She gave me a hint that was just very useful.
The hint was: 'When you add 2 + 2 you get 4. When you multiply 2 $\times$ 2 you get 4. You are looking for a number that you can multiply and add together that gives you the same answer.'
Afterwards I tried a bunch of ways and finally I got the answer which is:
1 + 2.175 + 2.705 = 5.883375 which also equals to 5.88 [correct to 2 decimal places]. You can see this on the rest of the page.
(Note that for each line Erin has chosen three numbers whose sum is 5.88, but then worked out their product, rather than their sum.)
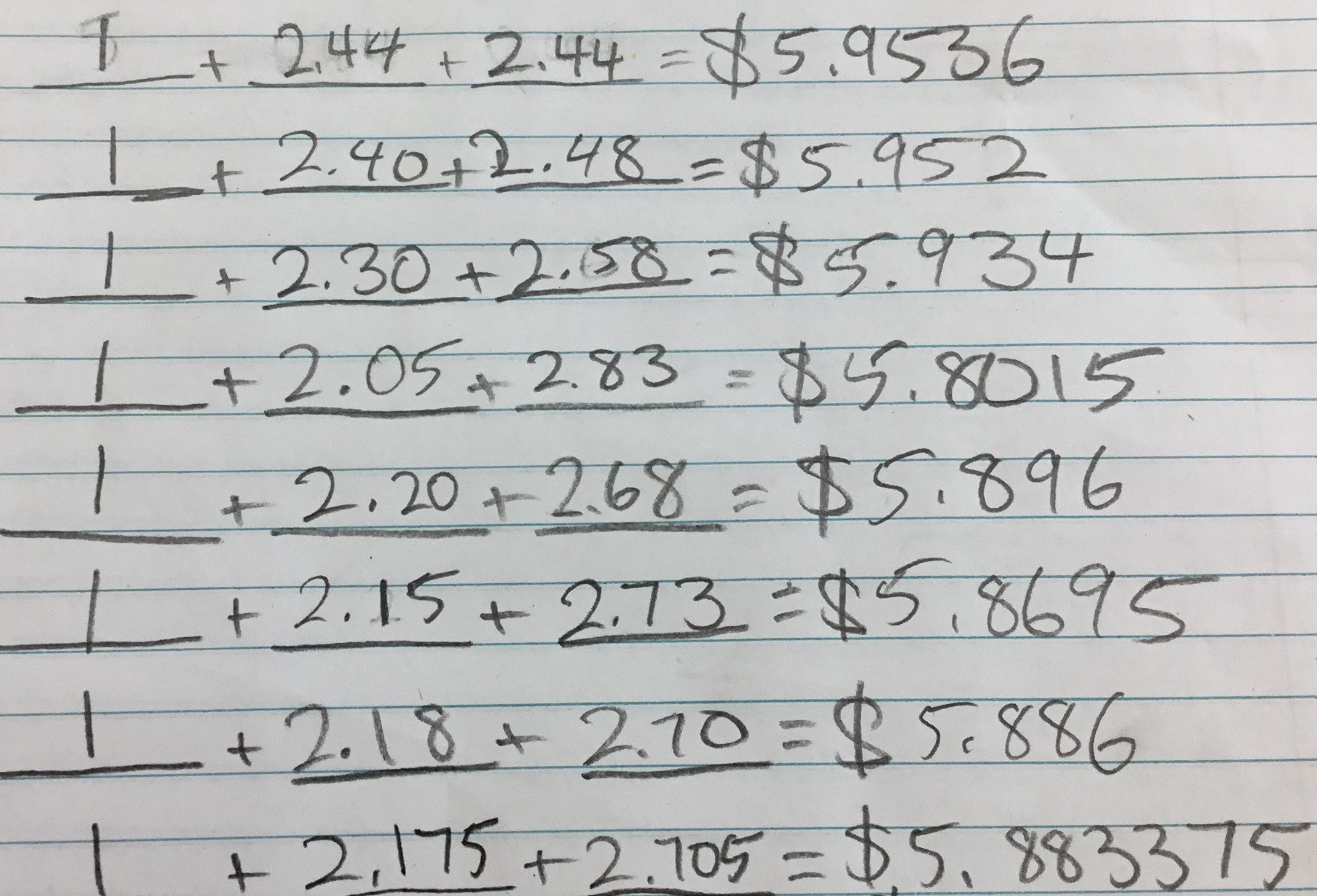
Well done, Erin - the numbers 1, 2.175 and 2.705 do add and multiply to 5.88. However, they cannot be the prices of items in a shop, because £2.175 is £2 and 17.5p (or, $ \$ $2.175 is $ \$ $2 and 17.5 cents), which is impossible.
Siddhant from Indus International School of Bangalore in India and Luis from King's College Alicante in Spain used Alison's second method. This is Siddhant's work:
From the information given, we know:$$a + b + c = 5.88\\
a \times b \times c = 5.88$$
In order to make the problem easier, we must convert the amount from pounds to pence. This would make it:$$a+b+c = 588\\
a \times b \times c = 5880000$$
Luis explained these conversions:
The value of the three items must add up to, for example, 588p (same as £5.88 but without the decimal) but therefore multiply to make 5,880,000, because if we turn the value of each item into pence, we must multiply each one by 100 (10 ²). This means that we must multiply 5.88 (the product) by 10â¶, because there are 3 items, and
10 ² $\times$ 10 ² $\times$ 10 ² = 10â¶.
Siddhant continued:
We must then find the factors of 5,880,000. The factors are:
2,2,2,2,2,2
3
5,5,5,5
7,7
Now, we must arrange these factors in such a way that when multiplied, they add to 588.
One way of doing this is by using the unit digit (8) to our advantage. We know that 2 cubed is 8, and therefore we would need multiples of 10 to get to the sum of 588.
However, [when one of the numbers is 8,] there is no combination of [the other factors] which [sums] to exactly 588, as it was either too big or too small. Therefore, it becomes apparent that we have to increase the number ending in 8. One way of doing this is by one number being 98 (7$\times$7$\times$2). That leaves us with 490 to get.
After a number of possible combinations, the other two numbers are:
250 (5$\times$5$\times$5$\times$2) & 240 (2$\times$2$\times$2$\times$2$\times$5$\times$3)
The three items are priced:
£2.40, £2.50, £0.98
Tong from the International School of Paphos in Cyprus used a similar method, but left all of the quantities in pence. Notice that this meant Tong had fewer factors to work with. Tong also used a bit more algebra to cut out some steps:
For $5.88$, we [multiply] by $100$ to get $588$, we factorise it into $(2\times2\times3\times7\times7)\div100$.
To get the last digit $0.08$, we have to divide one of the numbers by $100$. To get the "$8$" we have only two choices: either $(42\times2\times7)\div100=0.28$ or $2\times7\times7)\div100=0.98$.
Let's try $0.28$ first, $5.88\div0.28$ gives $21$ and $5.88-0.28$ gives $5.6$, we have two more numbers. We make them $x$ and $y$, so that $xy=21$, $x+y=5.6$, but that's not solvable.
Let's try $0.98$ then, $5.88\div0.98$ gives $6$ and $5.88-0.98$ gives $4.9$. We make $x$ and $y$ again. It's $xy=6$, $x+y=4.9$.
After solving this, we got that $x=2.4$ and $y=2.5$. Then that's the answer: $2.4$, $2.5$, $0.98$.
It is likely that Tong is using substitution to solve these simultaneous equations:
For $xy=6$ and $x+y=4.9$, $x+y=4.9$ can be rearranged to make $y$ the subject, so that $y=4.9-x$.
Substituting this into the other equation gives $x(4.9-x)=6\Rightarrow4.9x-x^2=6$, which can be rearranged to give $x^2-4.9x+6=0$.
Substituting $a=1$, $b=-4.9$ and $c=6$ into the quadratic formula $x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$ gives: $$x=\frac{4.9\pm\sqrt{4.9^2-4\times6}}{2}=\frac{4.9\pm0.1}{2}$$ so $x=2.4$ or $x=2.5$.
For $xy=21$ and $x+y=5.6$, $x+y=5.6$ can be rearranged to make $y$ the subject, so that $y=5.6-x$.
Substituting this into the other equation gives $x(5.6-x)=21\Rightarrow5.6x-x^2=21$, which can be rearranged to give $x^2-5.6x+21=0$.
Substituting $a=1$, $b=-5.6$ and $c=21$ into the quadratic formula $x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$ gives: $$x=\frac{5.6\pm\sqrt{5.6^2-4\times21}}{2}$$ But clearly $5.6^2-4\times21<0,$ so $\sqrt{5.6^2-4\times21}$ does not exist.
So these simultaneous equations cannot be solved.
For other shopping baskets
Shriya from International School Frankfurt in Germany used Alison's method for the next two baskets. Click here to see Shriya's concise solution.
Luis found three numbers for Alison's other two examples:
For the second problem, $ £5.49$, the value of the items were $ £1.25$, $ £1.80$ and $ £2.44$.
For the third problem, $ £5.55$, the value of the items were $ £1.85$, $ £1.20$ and $ £2.50$.
To work out the second and third problems, I again used Alison's method.
I noticed that, for the second one ($549$p), the unit was $9$, and so preferably two of my three items had to have units that together added to nine, in this case $5$ and $4$ ($125$ and $244$). Therefore, my final item had to end in a $0$, and so I used the $5$ and $2$ (which were both factors of $549$) to make the third item be a multiple of ten. I tried different combinations until my three items added up to $549$p.
I did the same thing for the third problem, $ £5.55$, but this time, instead of two of my three items adding up to the value of the unit of, in this case $555$p, I was able to achieve the $5$ (the unit) using $3$s and $5$s (which always give a unit of $5$ when multiplied). I again tried different combinations until my three items added and multiplied to get $5.55$
The value of the items of the extension ($ £7.11$) were $ £3.16$, $ £1.25$, $ £1.50$ and $ £1.20$. I used Alison's method again to work out the value of these $4$ items. One of the prime factors of $711,000,000$ (this time I had to multiply $7.11$ by $10^8$ because I had to work out the value of $4$ items, instead of $3$) was $79$, and so the only possible values for one item were:
$79 \times 2, 79 \times 3, 79 \times 2^2, 79 \times 2 \times 3$ and $79 \times 5$, because any other combination involving $79$ would exceed $ £7.11$, the value of the sum of the four items.
I started with the first possible value of the first item ($79 \times 2$) and got a unit of $8$. This meant that the value of another item had to have a unit of $3$ (so they add to $1$) assuming that the other two values were multiples of $10$. Once I saw that this didn't work, I tried with the second one: $79 \times 3$, and got a unit of $7$. This meant that the value of another item had to have a unit of $4$. I tried different combinations with the other items and realised that there was no possible way of making all four items add up to $ £7.11$.
Then, I tried with the third one: $79 \times 2^2$, and got $316$ (with a unit of six). This meant that the value of another item had to have a unit of $5$. After trying out different combinations, i found that $5^3$ was $125$. This was going to be the value of the second item, because on my last two items I used $5$s and $2$s to make multiples of ten, and once I did this, I tried different combinations with the remaining $2$s, $3$s and $5$s.
Finally, I discovered that $5^2\times 3 \times 2$ (third item) $+ 2^3\times 3 \times 5$ (fourth item) made $150$ and $120$ respectively. If we add $316$ (first item) and $125$ (second item) and $150$ (third item) and $120$ (fourth item), we get $711$. I then divided all of these values by $100$ and got the answer in pounds.
To prove that the costs giving rise to $ £7.11$ are unique (Very challenging extension) I tried out the other possible values of the first item ($79 \times 5$ and $79 \times 2 \times 3$) and I realised that because the value of $79 \times 5$ was so big ($395$), there was no way I could make the other items add up to $711$ using the numbers in $711,000,000$ expressed as a product of prime factors.
However, I tried all the different possible combinations, until I saw that not a single one worked. I then did the same with $79 \times 2 \times 3$ and with $79 \times 2^2 \times 3$ and these values were also big enough to prevent me from getting all the four items to add up to $711$p. Having tried all possible combinations for the value of the first item
($79 \times 2, 79 \times 2^2, 79 \times 3, 79 \times 2 \times 3,$ and $79 \times 5$) and after seeing that only one of them worked, I think I have proved that the costs giving rise to $ £7.11$ are unique.
Well done Luis - this almost proves it. Unfortunately you haven't shown that there aren't any other combinations where the final $1$ comes from adding $3$ of the units digits. For example, if one of the items cost $79\times3$ and had a units digit of $7$, Luis says that another item would need to have a units digit of $4$. But instead there could be two numbers, whose last digits are $2$ and $2$, or $1$ and $3$, or even $6$ and $8$.
Dominic wrote a program which finds all of the solutions - and in doing so shows that the one Luis found is the only one.
These are the basic steps of Dominic's program:
For each possible value of the smallest number,
For each possible value of the second smallest number,
For each possible value of the third smallest number,
Find the fourth number so that the sum is correct
Check whether the product is correct
If the product is correct,
Record this solution and then keep going through all of the possibilities.
This is how Dominic did it. This isn't the exact text of Dominic's program, but is pseudocode which you can easily convert into a programming language if you want to try it out!
Let 'total' = 7.11, 'product' = 7110000 (product in pence), and 'conversion factor' = 1000000 (conversion factor between products in pounds and pence).
The maximum value for the smallest number will be total/4 rounded to 2 decimal places.
For i = 0.01 to {total/4 rounded to 2 decimal places} in steps of 0.01,
The maximum value for the second smallest number will be a third of what's left - so (total-i)/2 rounded to 2 decimal places
For j = 0.01 to {(total-i)/2 rounded to 2 decimal places} in steps of 0.01,
The maximum value for the third smallest number will be half of what's left - so (total - i - j)/2 rounded to 2 decimal places
For k = 0.01 to {(total - i - j)/2 rounded to 2 decimal places} in steps of 0.01,
l = total - i - j - k
If i*j*k*l*conversion factor = product,
record/output/print i, j, k, l
end if
next/continue
next/continue
next/continue
This program actually outputs 6 solutions, but they are all the same 4 numbers in different orders. To rectify this, you could change the 'for' loops, so that j begins at i and k begins at j (instead of both beginning at 0.01). This will also make the program faster.
Jeremy, formerly of Epsom College, sent in a solution which didn't use Alison's ideas, but was a very concise way of solving the problem.
[$711=3^2\times79$,]
So a trial solution is (in pounds) $1 \times 3 \times 3 \times 0.79$ (we need $4$ factors).
However, this does not add up correctly (it adds to $779$ pence - but it is close).
Now we need to multiply each of the amounts by a multiplier $r_1$, $r_2$, $r_3$ ,$r_4$ so that $r_1\times r_2\times r_3\times r_4 = 1$.
The multipliers are simple fractions like $\frac12$ so that the new number is still a whole number of pence in each case.
For the first $3$ digits ($1$,$3$,$3$) we will only get totals of $150 $p, $100$p, $50$p, $25$p, $20 $p, $10 $p etc when we apply the multiplier - yet the sum must end in a $1$p.
So we will try $r_4 = 4$ (ie. take $4$ lots of $0.79$), as this ends in a $6$ ($4$ is the only multiple of $9$ that does end in a $6$ among the digits $1$ - $9$).
When combined with a $25 $p adjustment this gives a total ending in $1$p.
The only multiple of $9$ that ends in a $1$ is $81$ and $9$ lots of $0.79$ is too many to work, so this rules out the other adjustments to $ £1$, $ £3$ and $ £3$ which are multiples of $10$.
$( £1 \times \frac54) \times ( £3 \times \frac12) \times ( £3 \times \frac25) \times ( £0.79 \times 4)$ gives the correct answer:
$ £1.25 \times £1.50 \times £1.20 \times £3.16 = £7.11$
$ £1.25 + £1.50 + £1.20 + £3.16 = £7.11$
You may also like
Adding All Nine
Make a set of numbers that use all the digits from 1 to 9, once and once only. Add them up. The result is divisible by 9. Add each of the digits in the new number. What is their sum? Now try some other possibilities for yourself!
DOTS Division
Take any pair of two digit numbers x=ab and y=cd where, without loss of generality, ab > cd . Form two 4 digit numbers r=abcd and s=cdab and calculate: {r^2 - s^2} /{x^2 - y^2}.