 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Lost Books



While we were sorting some papers we found $3$ strange sheets which seemed to come from small books. They had once been used for wrapping and one side was very faded. The other side was in a language we did not know, but there were page numbers at the foot of each page.

Did the pages come from the same book, we wondered, and what numbers had been on the other sides of the sheets?
I decided to make a little book to see how the numbers worked. It had $4$ sheets which I folded to make $16$ pages. There was no need to staple it.
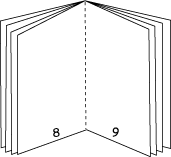
Then I made other little books, with both more and fewer pages. I made a table of my results and soon I knew how the numbering worked and could answer my own questions.
What answers do you think I got?
Later we found another sheet. The numbering on this was a bit different. Can you work out why?
