You may also like
Difference of Two Squares
What is special about the difference between squares of numbers adjacent to multiples of three?
Stage: 4 Challenge Level: 
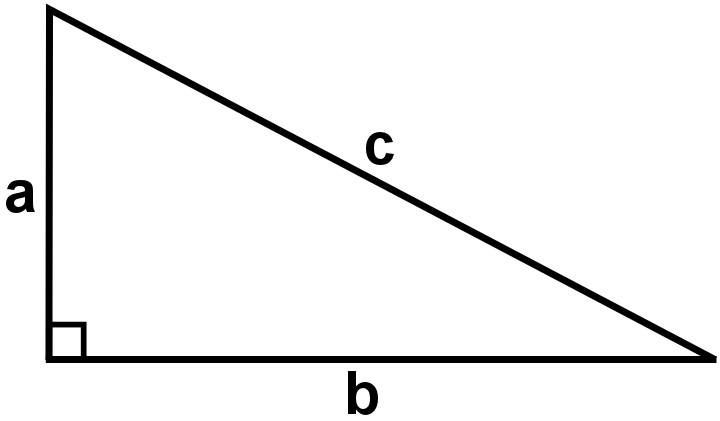
If this right-angled triangle has a perimeter of $12$ units, it is possible to show that the area is $36-6c$ square units.
Can you find a way to prove it?
Once you've had a chance to think about it, click below to see a possible way to solve the problem, where the steps have been muddled up.
Can you put them in the correct order?
a) Squaring both sides: $a^2+2ab+b^2 = 144-24c+c^2$
b) So Area of the triangle $=36-6c$
c) $a+b=12-c$
d) So $2ab=144-24c$
e) Area of the triangle $= \frac{ab}{2}$
f) By Pythagoras' Theorem, $a^2+b^2=c^2$
g) $a+b+c=12$
h) Dividing by $2$: $ab=72-12c$
Printable Version
Can you adapt your method, or the method above, to prove that when the perimeter is $30$ units, the area is $225 - 15c$ square units?
Extension
Can you find a general expression for the area of a right angled triangle with hypotenuse $c$ and perimeter $p$?
With thanks to Don Steward, whose ideas formed the basis of this problem.
Copyright © 1997 - 2018.
University of Cambridge. All rights
reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.
NRICH is part of the family of activities in the Millennium Mathematics Project.