Triangles in a Square
Problem
Triangles in a Square printable sheet
You may wish to print a dotty grid to work on this problem.

Here is a triangle drawn on a $5$ by $5$ dotty grid by joining the top-right-hand dot to a dot on the left hand side of the grid, and a dot on the bottom of the grid.
Here are some more triangles drawn in the same way.
Which has the largest area?

Now, think about the different triangles that can be formed with a vertex at $(5,5)$, a vertex on the left hand side and a vertex on the bottom of the grid.
What is the smallest area such a triangle can have?
What about the largest area?
Which areas in between is it possible to make?
Can you find a general expression for the area of a triangle on this grid if its vertices have co-ordinates $(5,5)$, $(x,0)$ and $(0,y)$?
What can you say about the areas of triangles drawn on a $6$ by $6$ grid? Or a $7$ by $7$ grid? Or a $100$ by $100$ grid...?
With thanks to Don Steward, whose ideas formed the basis of this problem.
Getting Started
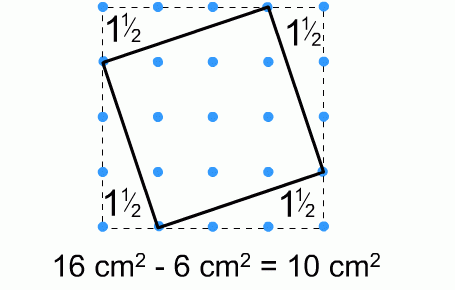
One method for working out the areas of the triangles is the 'boxing in' method:
Box in the chosen shape, work out the area of the box, and then subtract the unwanted areas in order to work out the desired area.
The example below shows how this method can be used to work out that the area of the tilted square is 10 cm$^2$.
Student Solutions
We had lots of great solutions to this problem. Thank you to all of you who wrote in!
Julian from the British School Manila, Ahrus and Ben from Dixons Trinity Academy, and Kira from Wycombe High School all managed to find the area of each of the coloured triangles on the $5 \times 5$ grid. Here's what Kira did:
How to calculate the area of each triangle:
When the triangles are drawn on the dotty paper they are surrounded by $3$
right-angled triangles. The total area of all three right-angled triangles
must be subtracted from the area of the square ($25$ squares) to give the
area of the triangle.
Red triangle is $10.5$ squares
Yellow triangle is $10.5$ squares
Blue triangle is $11.5$ squares
Green triangle is $11$ squares
Purple triangle is $10.5$ squares
Therefore the blue triangle has the largest area.
Jurmana, Haidi, and Nour from the Continental School Cairo all found the largest and smallest triangles they could make on a $5 \times 5$ grid:
The largest area I found was $12.5$ cm$^2$ when the corners of the triangle are at $(0,0)$, $(0,5)$ and $(5,5)$.
The smallest area I found was $2.5$ cm$^2$.
Here's how Julian found a general formula for the area of a triangle with vertices at $(5,5)$, $(0,y)$, and $(x,0)$:
Area of the top left white triangle:
base: $5$
height: $5-y$
area: $\frac{5(5-y)}{2}$
Area of the bottom left white triangle:
base: $x$
height: $y$
area: $\frac{xy}{2}$
Area of the bottom right white triangle:
base: $5-x$
height: $5$
area: $\frac{5(5-x)}{2}$
Since the area of the colored triangle is $25$-(the area of the three
triangles covering the white space), we can add the three areas and
subtract it from $25$.
This will give us an area of $\frac{5x+5y-xy}{2}$.
Victor from Dulwich College Seoul found this formula and used it to find all the possible areas of triangles on a $5 \times 5$ grid:
The possible areas are $2.5cm^2$, $4.5cm^2$, $5cm^2$, $6.5cm^2$, $7.5cm^2$, $8cm^2$, $8.5cm^2$, $9.5cm^2$,$10cm^2$, $10.5cm^2$, $11cm^2$, $11.5cm^2$, $12cm^2$, $12.5cm^2$ which is a total of $14$ areas.
Kira thought about triangles on bigger grids:
When a triangle is drawn in a $6$ by $6$ grid the area can be represented by
$3x + 3y - 0.5xy$.
When a triangle is drawn in a $7$ by $7$ grid the area can be represented by
$3.5x + 3.5y - 0.5xy$.
This shows that there is a pattern for finding the area of the triangle. $x$
and $y$ are multiplied by half of the number of squares up or down.
Let $n$ represent size of grid eg $7$ by $7$ grid is when $n=7$:
Area of triangle in square = $0.5nx + 0.5 ny - 0.5xy$ squares.
Teachers' Resources
These printable resources may be useful: Triangles in a Square, Dotty Grid.
Why do this problem?
This problem offers students a good opportunity to practise working out areas of triangles while using their visualisation skills to consider how to maximise and minimise the shaded area.
Possible approach
You might like to hand out this worksheet, and some dotty paper.
Start by displaying the red triangle, and invite students to estimate its area, perhaps starting by asking whether they think that more or less than half of the dotty grid is covered.

Once students have estimated the area, discuss how they might work out the area exactly. If no-one suggests it, invite them to consider subtracting the areas of the three unshaded triangles from the total area of the square grid.
Once everyone understands the method for working out the area of such triangles, invite them to find which of the four coloured triangles has the largest area. Again, they may wish to estimate the areas first.
Next, invite them to find all the possible areas of triangles with one vertex at (5,5), one on the left side of the grid and one on the bottom.
Finally, students could work towards an answer to the question "Can you find a general expression for the area of a triangle on this grid if its vertices have co-ordinates (5,5), (x,0) and (0,y)?"
Key questions
Is it easier to work out the shaded area or the unshaded areas?
If I know the total area and the unshaded area, how can I work out the shaded area?
Is it possible to cover more than half the area of the grid with a triangle?
Possible support
Isosceles Triangles offers practice in working out areas of triangles on a coordinate grid.
Possible extension
Students could go on to explore the areas of triangles drawn on larger grids, or take a look at Quadrilaterals in a Square
