Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Age 16 to 18
Published 2014
Probability Questions as Counting Problems
I think it is fair to say that, like its sister subject Statistics, Probability in STEP is significantly more disliked than most topics. However, also like Statistics, I think it is also often a misunderstood subject area. You really need very little mathematical expertise to attempt the Probability questions in STEP. There's no requirement to memorise or understand pages of formulae or many complex concepts; something I'm sure most readers will appreciate! Indeed, often all you need to be able to do is count, and determine precisely what a question wants you to compute mathematically. Thus, here, we will quickly review counting in probability before proceeding to put this skill to use in an example question.
Counting in Probability
Most often, we will simply be interested in determining the chance, or probability, an event of interest occurs. Doing so fortunately only requires us to count the number of ways that event can occur, out of the total number of things that can happen. Let's restate that a bit more formally: suppose we have a random variable \(X\), that can take any value from some possible list of options \(\Omega\). Then if we want to compute the probability some event \(A\) occurs, we need only determine how many elements are in \(A\) in comparison to how many are in \(\Omega\).
As always in maths, this can be made much clearer with an example. Let's take our random variable \(X\) as rolling a single die. Then \(X\) can take the values \( \{1,”¦,6\} \); this is our \(\Omega\). Suppose our event of interest is rolling an even number, i.e. \(A=\{2,4,6\}\). So:
\(\hspace{1.35 in} \mathbb{P}(X \in A)=\mathbb{P}(A \hspace{0.05 in} \text{Occurs})=\frac{\text{Number of elements of} A}{\text{Number of elements of} \Omega}=\frac{3}{6}=\frac{1}{2}. \)
This may be a particularly drawn out way to write down the chance of rolling an even number with a single die, but it is illustrates the key idea nicely: to compute probabilities, count!
Unfortunately, things will not be this simple in most of the questions put in front of us. Think for example about having to determine how many ways we could throw two heads out of three coin tosses, or draw two blue balls out of a bag containing four blue and five black balls. How do we do this? Fortunately, there are some standard formula that come in handy here; and moreover we can relate them all to drawing m balls out of a bag containing n distinguishable balls. You should try to convince yourself about why the following are the case:
- Drawing balls with replacement and with ordering: Then there are \(n^m\) possible ways.
- Drawing balls without replacement and with ordering: Then there are \({}^nP_m=\frac{n!}{(n-m)!}\) possible ways.
- Drawing balls without replacement without ordering: Then there are \({}^nC_m=\frac{n!}{(n-m)!m!}\).
The next article in this module puts some of the above formulae to the test in a past STEP question. For now however, let's solidify the idea of counting with a simpler example: what is the probability that a poker hand shows five different face values? To compute this probability we need to determine how many possible hands there are (of 5
cards out the 52 in a standard pack) that contain different face values, and how many total possible hands there are. The latter is simple, we simply use the third of formula above; it will be given by \({}^{52}C_5\). For the former, the best way to think about the number of possibilities is to think about choosing 5 face values of the possible 13 that are different, and then picking the suits
for each of these five cards, i.e. we have \({}^{13}C_5 \times 4^5 \) ways. Therefore our required probability is just:
\( \hspace{1.5 in} \mathbb{P}(5 \hspace{0.05 in} \text{different face values in a Poker hand}) = \frac{{}^{13}C_5 \times 4^5}{{}^{52}C_5}. \)
\( \hspace{1.5 in} \mathbb{P}(5 \hspace{0.05 in} \text{different face values in a Poker hand}) = \frac{{}^{13}C_5 \times 4^5}{{}^{52}C_5}. \)
Back to Basics
No discussion of Probability would be complete without giving acknowledgement to some of the most basic ideas behind it. How do we compute the probability of one or more events occurring? What does it mean for events to be independent? What about mutually exclusive? These should hopefully be familiar ideas, but if anything below looks unfamiliar make sure to brush up on your A-Level notes:
- \( \mathbb{P}(A \hspace{0.05 in} \text{or} \hspace{0.05 in} B)=\mathbb{P}(A \cup B)=\mathbb{P}(A)+\mathbb{P}(B)-\mathbb{P}(A \cap B), \)
- \( \mathbb{P}(\text{Not} \hspace{0.05 in} A)=\mathbb{P}(A^\text{c} )=1-\mathbb{P}(A), \)
- \(A\) and \(B\) are independent if \( \mathbb{P}(A \cap B)=\mathbb{P}(A)\mathbb{P}(B), \)
- \(A\) and \(B\) are mutually exclusive if \(\mathbb{P}(A \cap B)=0. \)
Conditional Probabilities and Bayes' Theorem
In STEP, one other major component of Probability questions is left to discuss; how to compute conditional probabilities and how to employ Bayes' Theorem. Not content with simply computing the probability of an event, we will often be interested in the chance something occurs, given prior knowledge of another event having occurred. We call such a probability a conditional one and to find the probability \(A\) occurs, given \(B\) has, we use the following formula:
\( \hspace{2.38 in} \mathbb{P}(A \hspace{0.05 in} \text{given} \hspace{0.05 in} B)=\mathbb{P}(A|B)=\frac{\mathbb{P}(A \cap B)}{\mathbb{P}(B)}. \)
By multiplying up we acquire what is sometimes referred to as the multiplication rule:
\( \hspace{2.1 in} \mathbb{P}(A \cap B)=\mathbb{P}(A|B)\mathbb{P}(B)=\mathbb{P}(B|A)\mathbb{P}(A). \)
This rule comes to prominence when you use tree diagrams. If you are faced with a STEP Probability question involving multiple events that happen in sequence, tree diagrams can be your best friend. Suppose for example that you know \( \mathbb{P}(A)=1/3, \mathbb{P}(B|A)=1/2, \mathbb{P}(B|A^\text{c})=2/3 \), and want to compute \(\mathbb{P}(B)\). Then we can combine this information into the following tree diagram where we use the multiplication rule on each branch:
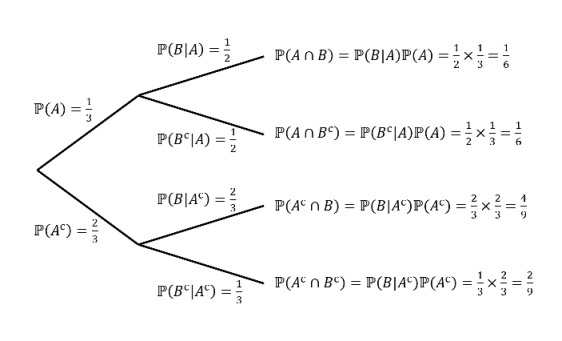
Then adding the trees where \(B\) occurs gives us:
\(\hspace{1.2 in} \mathbb{P}(B)=\mathbb{P}(B|A)\mathbb{P}(A)+\mathbb{P}(B|A^\text{c})\mathbb{P}(A^\text{c})=(\frac{1}{2} \times \frac{1}{3})+(\frac{2}{3} \times \frac{2}{3})=\frac{11}{18}. \)
A final acknowledgement now must be given to Bayes' Theorem, formed out of the multiplication rule. This states that:
\( \hspace{3.0 in} \mathbb{P}(A|B)= \frac{\mathbb{P}(B|A)\mathbb{P}(A)}{\mathbb{P}(B)}.\)
Often, the components of the right hand side will be much easier to compute than the left!
Summary
So, hopefully you're feeling at least a little more confident about Probability in STEP questions now: there really isn't too much maths you need to recall. Remember, think carefully about what the question is asking you to compute and then put your counting skills to good use! The rest is simply practice, and now seems like the perfect time to start: why not have a go at some problems yourself?