Path to the stars
Problem
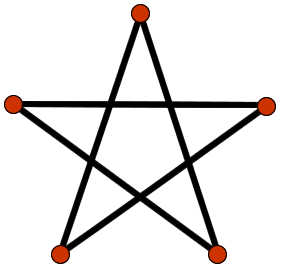
Is it possible to draw a 5-pointed star without taking your pencil off the paper?
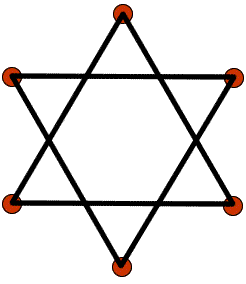
Is it possible to draw a $6$-pointed star in the same way without taking your pen off? Remember that you shouldn't join points that are right next to each other and you can't go over the same line twice. Your lines must run straight from one point of the star to another.
Have a go:
What about $7$-pointed and $8$-pointed stars?
Do you think you'll be able to draw a $9$-pointed star without taking your pencil off? Why?
Getting Started
When you try to draw a star, one way to begin is to join the first dot to the third dot i.e. miss out one dot each time as you go around. Why can't you draw a 6-pointed star in this way?
Now think about another way to draw the star. Does this work for a 6-pointed star?
Try to apply this to stars with more points and you should see the pattern!
If you go to the Printable Resources page, you can open and print PDF files of the circles (Circle templates > Without central point).
Student Solutions
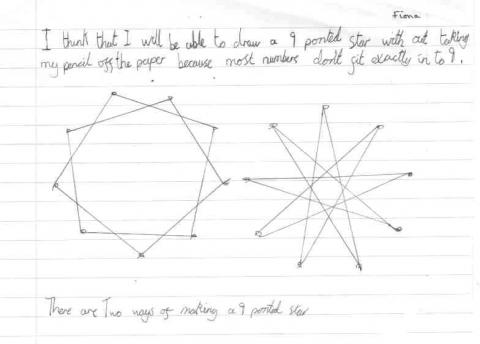
Fiona from Tattingstone has sent us her drawings:

She then goes on to predict whether she will be able to draw the $9$-pointed star and gives a good explanation:
Liam, David, Joseph, Matthew, Chris and Yuji at Moorfield Junior School have also begun to think about why you can draw some stars but not others. They say that for any odd number of points you start at any dot and then miss one out and join a line to the next one. Then you go from that dot to the one after the next. You keep repeating this, but only some even numbers work.
Matthew, Chris and Yuji say that even numbers work if you skip out two dots each time. They go on to say that this doesn't work for numbers in the three times table, which is why we can't draw a $6$-pointed star.
