Copyright © University of Cambridge. All rights reserved.
'Home Time' printed from https://nrich.maths.org/
Show menu
Alice, Beccy, Craig, David, Ellie and Francis all go to the same school. Usually they catch the bus home, but today they are staying later for hockey club. Alice lives the closest to school, so they walk round there and her mum gives the others a lift home.
The map below shows how the children's houses are connected by road (it is not to scale!). To make things easier, just the first letter of each name has been used.
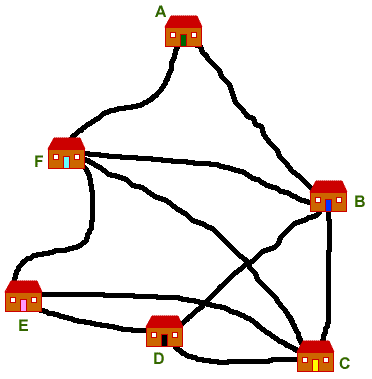
Alice's mum sets off from their house (A) with all the children. She needs to go to each house just once and then back home again. How many different routes are there?
In the end, she took a route like this:
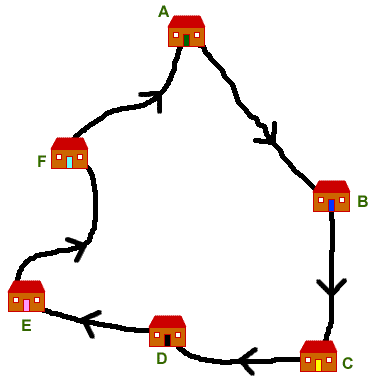
The entire journey took $1\frac{1}{2}$ hours and she was travelling at an average speed of $30$ miles per hour.
The total distance from A to D is the same as the total distance from E to A, which is $19$ miles.
It took twice as long to get from B to D as it did from D to E.
A is twice as far from F as it is from B.
The distance between A and B is a third of the distance between C and E.
Using this information can you find out how long each road is on the route taken by Alice's mum?