Copyright © University of Cambridge. All rights reserved.
'Getting Round the City' printed from https://nrich.maths.org/
Show menu
This resource is part of "Dotty Grids - Exploring Distance"
Getting Round the City printable sheet
The grid below represents a city laid out in "blocks" with all the roads running north-south, or east-west.
Imagine two friends live where the red and blue dots are on the grid.
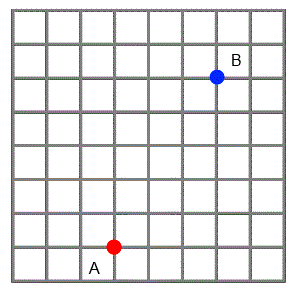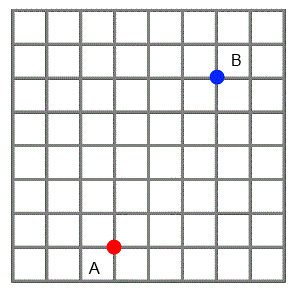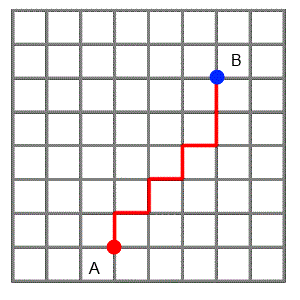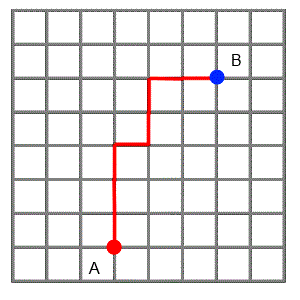
The animation shows three paths that one friend could choose if he wanted to visit the other. He likes to find the shortest routes possible, so he always travels north or east, never south or west.
What interesting mathematical questions could you explore on a city grid like this one?
Click below for some ideas.
How many different paths are there from A to B?
If I know the coordinates of two points, can I quickly work out how far I will have to walk to get from one to the other?
Is there a quick way to find all the different paths from one point to another?
Is there a quick way to work out how many different paths there will be?
If I start at a point and only want to walk 6 blocks, how many possible places might I end up?