 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Disappearing Square



- Problem
- Getting Started
- Student Solutions
Several teachers didn't like this trick but is it really a trick? When the rotation takes place the grid lines up along the slopping sides but does it exactly fit? When you count the squares the second time what are you counting? The counting may not be accurate. Are the 'half' squares all exactly half?
Many of you were puzzled by this. What is really going on here? We can't 'make' an extra square of area just by chopping a shape up and putting the pieces together differently so what is happening? William from Tattingstone describes it like this:
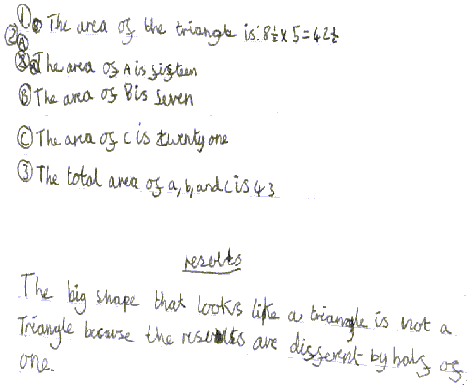
I think he is trying to tell us that the rectangle C doesn't quite fit in there. The line on the sloping side of the triangle isn't really a straight line is it? Measuring is never absolutely accurate is it?