Copyright © University of Cambridge. All rights reserved.
'Mystery Matrix' printed from https://nrich.maths.org/
Show menu
Mystery Matrix
Have a look at this table square or matrix:
Can you see how it has been constructed?
Why are some numbers in black and some in red?
Can you explain why the red 6 is in that particular square?
Why is there a 45 in the bottom right-hand corner?
You will notice that the numbers 2 to 9 are used to generate the matrix and only one of these numbers is used twice (the 2).
Can you fill in the matrix (table square) below?
The numbers 2 to 12 were used to generate it with, again, just one number used twice.
You might like to have a go at similar versions of this task using the interactivity below.
Once you've worked out what each heading must be, drag the purple numbers to the appropriate spaces. When you think you have cracked it, click "Show the solution" to see if you are right.
For an extra challenge, you could try this 6 by 6 version of the grid.
You may like to try Missing Multipliers once you've had a go at this task.
Why do this problem?
One way to encourage children to be more curious is to present them with challenges to be solved, or intriguing contexts that require explanation.This problem requires learners to apply knowledge of multiplication facts, and stresses the importance of knowing the squares of numbers, particularly the squares of primes. It will increase their familarity with representing multiplication facts as a grid or matrix.
Possible approach
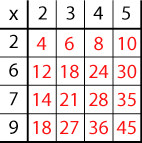
You could start by giving the whole group some numbers such as $18$, $33$, $35$, $48$ and $56$ and asking for the multiplication facts that generate them. Include some squares such as $25$, and even $49$, if you feel the group might have a problem identifying it.
You could then introduce the first matrix given in the top example and get the group to help fill it in. Point out the 4 which is generated by 2x2 and therefore a square and the only number which has been used twice. As you go round, ask the learners how they know which number should go in the various square spaces. You could make a list of all the numbers from 2 to 9 and cross them off as
they are used. As an alternative, you could give them the completed example and ask them to talk about it in pairs so that in a whole-group discussion, you come to an agreement about how the matrix represents these multiplication facts. All this should help them to be able to tackle the main part of the problem with confidence.
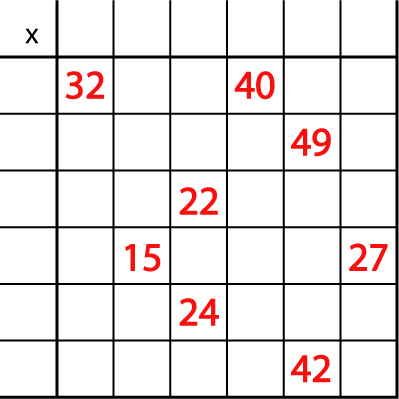
After this learners could work in pairs on the problem itself so that they are able to talk through their ideas with a partner. They could use this sheet which has two copies of the matrix on it.
At the end of the lesson the whole group could come together again to discuss, not only the answers, but how they worked them out and which multiplication tables they needed to know well in order to do a problem such as this.
The interactivity could be used to round off the lesson. Can the class use their knowledge of times tables and the strategies they have developed to work out the headings of the rows and columns?
The interactivity could also be used in its own right during subsequent lessons, perhaps with learners working in pairs on a computer or tablet.
The interactivity could be used to round off the lesson. Can the class use their knowledge of times tables and the strategies they have developed to work out the headings of the rows and columns?
The interactivity could also be used in its own right during subsequent lessons, perhaps with learners working in pairs on a computer or tablet.
Key questions
Where might you start? Why?
How can you decide which number is used twice?
Which multiplication table does that number come into? Is that the only table it is in?
How can you keep a check on which numbers you have used?
What are you curious about?
What are you curious about?
Possible extension
Learners could make a similar challenge with the least amount of information given so that it can still be done. They could then swap with someone else. Missing Multipliers would make a great follow-up to this one.