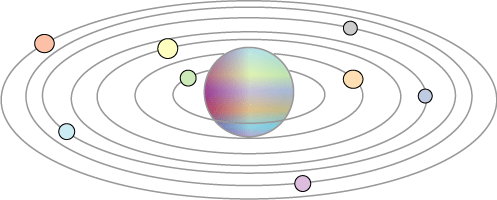
Copyright © University of Cambridge. All rights reserved.
'The Moons of Vuvv' printed from https://nrich.maths.org/
Show menu
The Moons of Vuvv
The planet of Vuvv has $7$ moons which lie spread out on one plane in a great disc round it. These Vuvvian moons all have long and confusing names so scientists usually call them by their initials: $A, B, C, D, E, F$ and $G$ starting from the nearest one to the planet.
When two of these moons line up with the planet it is called a 'lunar eclipse'. When three line up with the planet it is called a 'double eclipse', when four do it is a 'triple eclipse' and so on. Once in a while all seven moons line up with the planet and this is called a 'super-eclipse'.
Moon $A$ completes a cycle round the planet in one Vuvvian year, moon $B$ takes two years, moon $C$ takes three years, moon $D$ takes four years and so on.
How long is it between each 'super-eclipse' on the planet of Vuvv?
Why do this problem?
This problem offers opportunities for pupils to reinforce their understanding of factors and multiples, and, in a simple example, see an illustration of 'lowest common multiple'. It would fit in well when revising multiplication tables or working on multiples and factors.
Possible approach
You could start on this problem with a whole class activity counting in, for example, $2$s and $5$s. When do you say the same number in both? Try also two numbers which have a common factor, for example, $4$s and $6$s. When do you say the same number first in both?
After this you could introduce the problem either verbally, as a printed sheet or on an interactive whiteboard. Once the children have understood what they are to do, they could work on it in pairs. Some children might benefit from using a calculator for this activity both for multiplying by $7$, and for checking results. You may wish to stop the class part way through to share some of the
different ways they are working and recording. Some may be drawing pictures, others may be listing numbers. You could talk about the benefits of the different ways and it may be that some children adopt other representations following this sharing process.
A discussion of methods and comparison of answers in a plenary may well bring up different results. This would be a good opportunity to discuss the meaning of lowest common multiple.
Key questions
How many years does it take for these two moons to coincide?
Do these two moons coincide sooner than that?