Introduction
At NRICH, our aim is to offer rich tasks which develop deep understanding of mathematical concepts.  Of course, by their very nature, rich tasks will also provide opportunities for children to work like a mathematician and so help them develop their problem-solving skills alongside this conceptual understanding. Such tasks also provide valuable opportunities for you to assess where children have got to in their thinking and so support the next steps on their learning journey.

The current National Curriculum in England, which became statutory in September 2014, contains more content related to fractions than the previous curriculum. To support children in getting to grips with the concept of fractions it is important to make sure they have lots of practical and varied experience using objects, shapes and quantities. This, combined with an experience of rich tasks that stimulate and challenge their thinking; the opportunity to talk and the chance to use models and images rather than 'tricks', will all support their growing understanding of fractions.


Why might children find fractions difficult?
Difficulties with fractions often stem from the fact that they are different from natural numbers in that they are relative rather than a fixed amount - the same fraction might refer to different quantities and different fractions may be equivalent (Nunes, 2006).  Would you rather have one quarter of £20 or half of £5? The fact that a half is the bigger fraction does not necessarily mean that the amount you end up with will be bigger. The question should always be, 'fraction of what?'; 'what is the whole?'. Fractions can refer to objects, quantities or shapes, thus extending their complexity. 

In order to be able to develop their understanding and then generalise about fractions, children need to explore many representations and uses over a significant period of time.  In the Early Years, learners will have learnt to generalise the concept of three by having lots of experience of the three-ness of three, yet with fractions we may find in school that their experience is limited to pizzas, sticky paper and chocolate! Do the children have experience of objects, shapes and amounts in equal measure and do they have experience of the whole being something other than 'one'?

In our Fractions Feature, of which this article is a part, we offer links to two groups of tasks:

• The first group gives you some starting points to explore with your class, which are applicable to a wide range of ages.  The tasks in this first group will build on children's current understanding of fractions and will help them get to grips with the concept of the part-whole relationship. 
• The second group of tasks focuses on the progression of ideas associated with fractions, through a problem-solving lens.  So, the tasks in this second group are curriculum-linked but crucially also offer opportunities for learners to develop their problem-solving and reasoning skills.   

In this article, we will discuss each group of tasks in turn, outlining further reasons for grouping in this way and explaining why each particular task has been selected.


First Group of Tasks - Starting Points
As mentioned above, all these tasks could be introduced to children of any age.  They provide a chance for meaningful mathematical discussion and sharing of current understanding, in addition to offering opportunities for challenging misconceptions.  It is important that children build up a vocabulary with which to talk about fractions.  Of course this is a gradual process, but greatly helped by you modeling appropriate language wherever possible and drawing attention to good use of specific vocabulary by children themselves.  All of the following tasks provide contexts in which to encourage learners to talk about their ideas and to work towards refining their vocabulary.  (The article Developing a Classroom Culture That Supports A Problem-solving Approach to Mathematics offers several practical ideas to help your classroom become a classroom that is based on talk.)

Paper Halving is a wonderfully rich task which needs only a plentiful supply of plain A4 paper.  Learners are invited to halve pieces of paper in different ways and to articulate how they know that they have created halves.  Talk is key here.  Asking children to explain their ideas will help to reveal their understanding even if their constructions are not quite accurate.  You can facilitate discussion about not all halves being symmetrical and it would also be fruitful to ask how learners think the task would have been affected if they had been given squared paper rather than plain. 

 What Do You See Here? builds on Paper Halving by having a range of sizes of paper along with their related halves.  In a similar way to Paper Halving, this activity encourages learners to explore fractions as area.  Children are invited to 'say what they see' to prompt discussion related to statements about the paper.  Here, the teacher's role is to draw out the idea that the 'halves' are different sizes (“I'll have the bigger half!”), as the idea of a half is meaningless without knowing the whole.  In this way, the task lays the foundations for a deep understanding of the part-whole relationship.

(In our Early Fraction Development article, which is also part of the first group of resources in this feature, Bernard Bagnall describes his experiences of using these two tasks, and others, many times with groups of children and suggests further ideas using paper.)

And how often do we vary the 'whole'?  Is it always 'one'?  What about sharing two pizzas between three?  In the NRICH task Chocolate, the 'whole' is one, two or three bars of chocolate.  Learners have to make a decision about the best table to stand at if the chocolate on it is shared between everyone at that table.  Encouraging children to record their ideas themselves helps us 'see' their thinking and assess what they are doing.

Fractions as a form of division
In her research, Nunes (2006) suggests that sharing situations might also be used as a starting point for children's understanding of fractions since she found that primary school children have some insights into fractions when solving division problems:


 Our Early Years Foundation Stage activity Maths Story Time introduces Pirate Panda, who has stolen all the treasure but Cat, Dog and Rabbit want some too.  What do the children think they should do?  In a similar way, the activity Fair Feast offers the context of sharing a picnic and could form the basis of an initial exploratory task.  You could also invite learners to consider other food types - can they choose something that they would like to bring to the picnic and explain how it could be shared?

In summary, the tasks that comprise the first group within our Fractions Unpacked Feature ”¦

• are applicable to a range of ages;
• provide contexts in which to explore the part-whole relationship in depth;
• offer opportunities to develop conceptual understanding through talk.

Second Group of Tasks - Progression in Fractions Through Problem-solving
The second group of tasks in our Fractions Unpacked Feature has been selected to reflect a progression in concepts associated with fractions at the same time as giving learners opportunities to develop their problem-solving and reasoning skills.

Being able to recognise, find and name 'a half' is often one of the first steps along the fractions journey and the tasks included above in the first group will be useful in that regard.  Also worth mentioning is the activity Halving which focuses on halving in the context of area (of squares).  A Bowl of Fruit, however, explores halving in the context of discrete objects and you could easily tweak the task to create similar problems focusing on slightly more challenging curriculum content by using the language of halves, quarters and/or thirds.

The idea of equivalence is a key one to introduce as children's understanding of fractions develops.  Not only are learners encouraged to find families of fractions that are equivalent, but also to recognise decimal equivalents of fractions.  Being able to round decimals to the nearest whole number is a skill that is often taught around this time, and the two tasks Round the Dice Decimals 1 and Round the Dice Decimals 2 offer meaningful practice.  These two exploratory tasks give learners the chance to investigate for themselves, to conjecture and to generalise, meaning that not only will children be getting better at rounding, but they will also be developing their reasoning skills too.

In Spiralling Decimals, learners are required to compare decimal numbers and the game context may provide motivation for some.  Trying to beat an opponent demands a higher level of thinking in terms of developing a strategy.  In deciding which number to choose for any one turn, pupils will perform multiple comparisons and select the one they believe is 'best' for that move.  Asking a pair to play another pair at this game means that partners can talk to each other about their thinking, which will help clarify their ideas.  (As opposed to an individual playing competitively against another individual when neither will want to give away their strategy!)

The activities Linked Chains and Fraction Lengths both offer opportunities to identify, name and write equivalent fractions, as well as to add fractions.  Fraction Lengths is slightly more challenging, as the denominators are not always multiples of the same number.  Both tasks have multiple solutions, so children are encouraged to use a variety of problem-solving skills, such as trial and improvement, and working systematically.

If you would like to focus on supporting children to consider how to go about solving a problem, Andy's Marbles may well fit the bill.  The task involves using fractions to calculate and divide quantities, and it is certainly not straightforward.  The level of challenge it provides means that it lends itself to referring specifically to one or more of the four stages of the problem-solving process (see the article Developing Excellence in Problem Solving with Young Learners).

When it comes to calculation of fractions, the danger is that we introduce rules to be memorised and suddenly the conceptual development appears no longer to be valued.  However, in the article Models in Mind, Mike Askew demonstrates that the array is a powerful tool for thinking about multiplication of fractions, giving children a visual image to draw on, rather than relying on 'tricks'.  He begins with an array such as this one, representing 13 x 4:

 

By chunking the 13 into 10 and 3, we can use known facts to solve this multiplication:

13 x 4 = (10 x 4) + (3 x 4)

Of course, as the numbers increase, it becomes tedious to draw out all the dots, so we encourage children to make use of a blank array.  For example, 15 x 4 could be represented as:

 

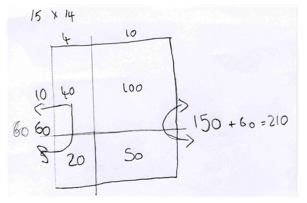
This leads into the grid method for multiplication.  Here is an image showing both the array and grid method for solving 14 x 4:

 

We can then see how multiplication of fractions follows on.  For example, to calculate $\frac{2}{3} \times \frac{2}{5}$, we would start with an array divided into thirds one way and fifths the other way:

 

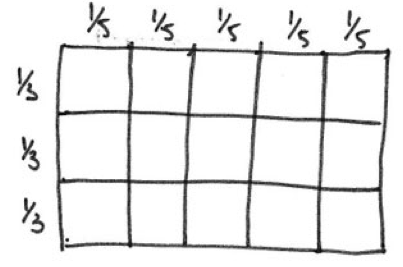
Learners who have come to think of multiplication in terms of arrays will be comfortable in thinking of the required piece as being the part of the array marked out by the intersection of the $\frac{2}{3}$ and $\frac{2}{5}$:

 

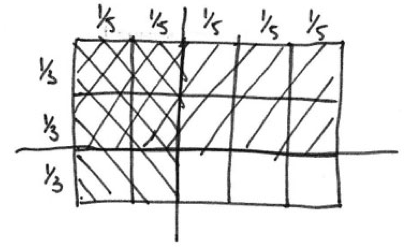
The article is well worth a read and reminds us that “the mark of a good model for/tool for thinking with is that it can help learners gain insight into mathematical structure, not simply get correct answers”.


Summary 
The concept of fractions is a complex one and it takes time, combined with a rich range of experiences and appropriate mathematical models, for children to develop a deep and rigorous understanding. You may like to try out some of the resources we have recommended in this article to see how they can support the development of children's understanding of fractions. You may also want to look to see what the children's 'fraction diet' is like across the whole school and how it could be usefully strengthened to maximise the opportunities children have to develop a meaningful and thorough understanding of fractions. 


Further reading on NRICH
Early Fraction Development
Models in Mind
History of Fractions
Manipulatives in the Primary Classroom

References
Nunes (2006) Fractions:  <link defunct 2019> Difficult but crucial in mathematics learning - www.education.ox.ac.uk/wordpress/wp-content/uploads/2011/04/resbrief_fractions.pdf