The solutions that arrived on our desk for Numerically Equal all had the same answer, but slightly different ways of finding it. Jack of Tattingstone Primary School sketched the stages of his thinking.

Chris used addition to help him with the perimeter calculation:

$4cm+4cm+4cm+4cm = 16cm$

Whereas, Sam of St Margaret's Primary School in Newcastle-under-Lyme, changed this to multiplication:

$4cm$ x $4$ (sides) $= 16cm$

Does this measurement of 4cm work for the area? According to Annice and Grace in Yarm Primary School, and Thomas it does! Backing them up with their answers were Jade and Marion both of Tattingstone Primary. Great explanations came from both girls.

Asher had the same idea as a Franco of Hazelwood School, London. Franco solved this "within a few minutes by thinking of square numbers and dividing them by 4". He hit upon a 4cm square as one possible answer but remains convinced it is not the only one and has gone to do further investigations on his own! Good for you Franco, let us know of any other solutions your investigations reveal.

There was a second challenge here, finding a rectangle that is twice as long as it is wide and that has an area and perimeter of 18 units. Daniel , Marion and Jade (all of Tattingstone School) had the same strategy that worked very well for each of them. Each drew a rectangle then drew the same size rectangle attached to it and calculated the area. Jack shows us a similar way to Marion and Jade's and how he can prove his answer.

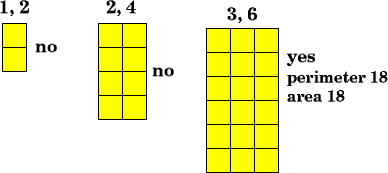
Christopher and James both explained in words and numbers rather than diagrams:

The perimeter will be $6+3+6+3$ which equals $18cm$.

The area is $6$ x $3$ which equals $18 cm^2$.