 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Red Balloons, Blue Balloons



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
There were many replies to the puzzle of the bursting balloons. You needed to be very clear about what you were being asked in this problem. Here is some advice about how to make sure you are clear from Joey and Vincent, both from Colindale Primary School in London:
We read the passage again and again until we understood the problem.
We know that at the beginning of Katie's seventh blow the balloon popped. The question was how many puffs did it take Will to burst the balloon? Some people told us how many puffs of air he blew in before it burst and others said which was the puff of air that was just too much for the balloon to take.
Several different answers were submitted. Was this the type of problem that has a single answer or do you think there could have been several solutions?
Different strategies and approaches were taken. Some people used their knowledge of addition, others used multiples and another group of problem solvers used their understanding of fractions to arrive at their solutions.
Allison explains a strategy using first a fraction and after that using addition.
To find out what was happening with Katie, we did this
$24 + 12 = 36$
$36 + 12 = 48$
$48 + 12 = 60$ ...
And so on ... $24, 36, 48, 60, 72, 84$ then Bang!
For Will
Half of $14$ is $7$.
You use this information and add.
So, $14 + 7 = 21$.
As Crewe, Errington and Porter and Croft explain:
So ... $14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84$ then Bang!
Jadie from Tattingstone School, shows how division was the operation that helped her find and answer.
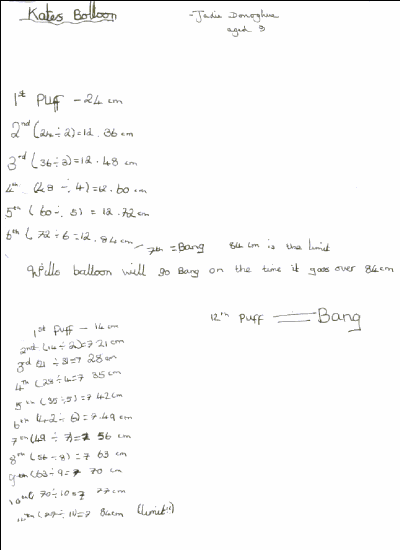
Joey and Vincent made use of what they know about fractions to find a solution:
Katie's first puff of the balloon measured a circumference of $24$cm then $\frac{1}{2}$ as much had to be added onto $24$cm. We found that half of $24$cm was $12$cm and we added it to $24$cm. That came to a total of $36$cm .We found $\frac{1}{3}$ of $36$cm and got an answer of $12$cm and added it to $36$cm. That gave us a total of $48$cm. We found a $\frac{1}{4}$ of that and we did the same thing for $\frac{1}{5}$, $\frac{1}{6}$.See the pattern beginning to unfold?
Verity explains her answer by finding a common multiple of 12 and 7:
I worked it out by working out the size of Katie's balloon as
she blew it up. The numbers went up in the $12$ times table. With
Will's balloon, the numbers went up in the $7$ times table. I wrote
out my $7$ times table until I found a number that was the same as
in Katie's list.
My lists looked like this:
| 24 | 14 |
| 36 | 21 |
| 48 | 28 |
| 60 | 35 |
| 72 | 42 |
| 84 | 49 |
| 7th blow | 56 |
| 63 | |
| 70 | |
| 77 | |
| 84 | |
| 12th blow |
Tom as well as Emily C, Emily G, Gabrielle and Rebecca from The Mount School think Will did $11$ puffs before his balloon burst. Or, as Verity puts it, what burst the balloon was the $12$th blow!
You may also like
Chocolate
There are three tables in a room with blocks of chocolate on each. Where would be the best place for each child in the class to sit if they came in one at a time?