 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Two Spinners



- Problem
- Getting Started
- Teachers' Resources
Two Spinners
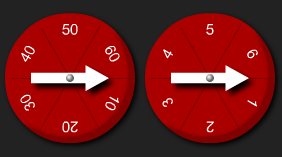
There are two spinners. The first spinner shows 10s and the second spinner shows 1s.
When you spin the two spinners, the numbers can be combined. For example, if the spinners land on 20 and 4, I can combine these numbers to make 24.
What two-digit numbers can you make?
What numbers can't you make?
There some interactive spinners that you might like to use for this problem. (You can choose to spin two spinners at the same time, and you could use one spinner to represent the tens digit and the other spinner to represent the ones digit.)
Why do this activity?
This activity reinforces the idea of partitioning numbers into 10s and 1s and recombining these. It encourages children to record their results, notice patterns and make predictions.
Possible approach
A possible starting point is with arrow cards to remind the class how to partition two-digit numbers into 10s and 1s, and how to combine 10s and 1s to make two-digit numbers.
The interactive spinners can be used to model the activity on an interactive whiteboard or can be used by the children as they engage with the task. You may also find that individual spinners or dice are useful. Stickers can be added to adapt pre-numbered or blank dice or spinners.
As the task is being modelled, the numbers that have been made could be marked off on a 100 square. This organisation of results will support the children to notice patterns in which numbers can and can't be made and their explanations of why this is the case.
Some children may move onto the extension tasks (below).
Key questions
Which numbers have you made?
Which can be made? Why? How many is this in total?
Which cannot be made? Why?
Possible extension
Extension 1: Having completed the original task, ask the children to look at the gaps on their 100 square and encourage them to work out out how the 10s and 1s spinners can be changed in order to make other numbers - and ultimately complete - the grid.
Extension 2: There could be different spinners with 10s and 1s, perhaps this time with 30, 40, 60, 70, 80, 90 and 1, 4, 5, 7, 8, 9. The children could again explore which numbers can and can't be made, and how many different numbers this is. They should be encouraged to compare their findings to the original task. What do they notice? Why does this happen? They may be able to make a
general statement about how many numbers can be made with two spinners (with unique entries).
Extension 3: This time the entries on the spinners might not be unique. So for example, the spinners might show 10, 10, 30, 40, 50, 70 and 2, 3, 5, 5, 8, 9. What numbers can be made this time? Compare the overall amount to the original task and extension 2. What do they notice? Why does this happen?
Extension 4: What happens if you introduce a 100s spinner as well?
Extension 5: What if you change the number of entries on the spinner (so that it is no longer a six-spinner)?
Possible support
Arrow cards will support the partitioning and recombining of 10s and 1s.
A 100 square will support children's recording.