Before reading this article, you may like to read Manipulatives in the Primary Classroom which offers research-based guidance about using hands-on equipment in the teaching and learning of mathematics.

Counters are such a readily available and versatile resource.  They can be used to represent a multitude of different things as well as often specifically featuring in mathematical problems and games in their own right.  In this Counters Feature, we draw your attention to a range of activities which require (to differing degrees) the use of counters. 

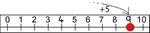In each of the three lower primary tasks, the manipulation of counters helps to embed understanding of a particular concept.  In Number Lines,  a counter is used to keep track of position on a number line and the act of 'jumping' along the line with the counter gives a physical model for addition and subtraction.  In turn, this physical model becomes a mental image for children to draw on in the future. This model also helps learners grapple with the fundamental ideas of doing and undoing in relation to addition and subtraction.

In Biscuit Decorations, different coloured counters could be used to represent the different decorations although this is just one way of approaching the problem.  It may be that children move a counter as they count along the biscuits, in which case this movement will help reinforce the idea of counting in twos/threes etc, or it may be that they use a finger to keep track and then place the counter once they have landed on the appropriate biscuit.  In either case, once the counters have been placed, the resulting picture gives a helpful visual image of the concept of multiples. 

Making Shapes also encourages formation of a mental image using the counters, this time of numbers as rectangles, leading to the concept of multiplication and factors/multiples.   Being able to physically create the rectangles will help children create and preserve their own mental image and also provides a 'shared memory' for you as the teacher to refer to on subsequent occasions.

In two of the three upper primary tasks in this Counters Feature the manipulation of counters also helps concept development.  In Bracelets, counters represent beads on a string and learners are challenged to investigate the shapes the bracelet could take.  Using counters helps reinforce the properties of shapes and the meaning of 'regular'.  Depending on the direction the pupils take, the counters may also help reveal connections between number patterns and shape, which could also extend to generalisation and a form of algebra.  Being able to move counters around to tackle this task is much less laborious than drawing and can 'free up' those children who find it hard to commit ideas to paper.

The second upper primary activity is also connected with shape.  Square Corners focuses on the properties of squares, as the name suggests!  Children often struggle to recognise a square which is not orientated in such a way as to have horizontal and vertical sides, and this problem is perfect for addressing that difficulty.  Here, counters represent the position of the corners of a square.  Being able to place them on a printed grid allows learners to 'play around' with arrangements, so might have the same 'freeing' effect mentioned for Bracelets.  It also enables pupils to rotate the grid and so compare arrangements easily.

The last activity in this Counters Feature is a game, First Connect Three.  Like many games, the use of counters in First Connect Three is to mark places on the board.  In this instance, the counters are not directly playing a role in concept development.  However, the aim of the game (to get three counters in a line), encourages players to consider likelihood and to tackle calculations involving negative numbers.  The counters are part of the game set-up, offering a motivating way to engage in probabilty and calculation.

There are plenty more activities involving counters here and a list of games in particular here.  You may also find it helpful to read the article Place Your Counters which was originally written for the Mathematical Association's journal, Equals.