 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Eleven



- Problem
- Student Solutions
There were several solutions sent in to this problem, which was about substituting numbers for letters. Most people interpreted the problem in the same way, that different letters could not share the same value, in other words H and E had their own value and E could not be the same as H. Well done to each of the solution finders.
Christina Ivanova, from Marlborough Primary School explained her strategy for keeping track of the digits she used and to help her discover the value for each letter.
I saw there were 10 different digits which meant there would be 10 different digits. From then on I started guessing the numbers, crossing off the digits as I used them. My final solution was:
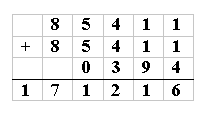
Christina's solution was shared by Ece Tugc and Simin Araz (Irmak Primary School, Istanbul, Turkey)
A second solution was found by Sophie and Annabelle (Annesley College, Adelaide, Australia), Sinan Ersanli (from the sixth grade of Irmak Primary School, Istanbul, Turkey) and Ece Demir (also in sixth grade, in the Irmak, Private Primary School). Sophie and Annabelle wrote it out in the following way:
T= 7
H = 4
F = 2
L = 5
R = 6
O = 0
V = 3
N = 8
E = 1
This is the sum with the letters replaced with the digits
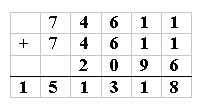
Simin Araz from Irmak Primary School in Istanbul, Turkey found a third solution to the problem:
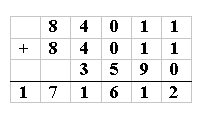
And Rose from Claremont Primary School in Tunbridge Wells submitted this solution, which was different to all the other ones that we had received.
Oliver, Amiko, Scott, Ben, Billee and Aidan, from Curdworth Primary School in the West Midlands, worked out one more solution:
T = 4
H = 6
R = 5
E = 1
F = 8
O = 2
U = 9
L = 0
V = 3
N = 7
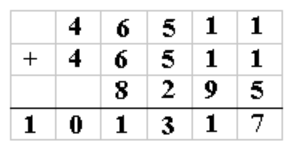
Well done to you all.
Are there any more solutions that could be found for this problem?
Well many years later we have a new solution and it's from the Down School in Kent. The teacher says that Archie, probably the youngest to have an answer, worked out that E must be 1 because T + T added to a 2 digit number and therefore he tried U as 9. After that he used trial and improvement. So here are his solutions.
T = 7; H = 8; R = 0; E = 1; O = 3; U = 9; L = 6; V = 4; N = 2
| 7 | 8 | 0 | 1 | 1 | |
| 7 | 8 | 0 | 1 | 1 | |
| 5 | 3 | 9 | 0 | ||
| 1 | 6 | 1 | 4 | 1 | 2 |
Thank you Archie, well done!
Are there still more to be found?
Are there any factors that limit the number of possible solutions?
Can anybody suggest a strategy for finding all the possibilities?
You may also like
Double Digit
Choose two digits and arrange them to make two double-digit numbers. Now add your double-digit numbers. Now add your single digit numbers. Divide your double-digit answer by your single-digit answer. Try lots of examples. What happens? Can you explain it?
Repeaters
Choose any 3 digits and make a 6 digit number by repeating the 3 digits in the same order (e.g. 594594). Explain why whatever digits you choose the number will always be divisible by 7, 11 and 13.
Big Powers
Three people chose this as a favourite problem. It is the sort of problem that needs thinking time - but once the connection is made it gives access to many similar ideas.