Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Watch Your Feet
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We received some fantastic solutions to this Bernard's Bag investigation. One of these came from Adam, from Milton Mount School. Children at Summercroft Junior School who go to the lunchtime Challenge Club sent us some very interesting work: Laura B and Adam sent this diagram showing the longest possible route for a path 3 paving stones wide and 14 long:
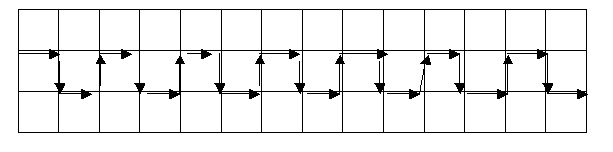
Along with Laura S, Eleanor and Oliver, the pupils at the club have taken the investigation further and begun to generalise. They have found a way to work out the number of "steps" in the longest possible route.
Laura S and Eleanor explain:
We found the longest route by taking the length (L), the amount of starting places there were (P) and then took (PxL) - (P-l) = The longest possible route.
Oliver, Laura S and Eleanor extended this to a path 4 paving stones wide:
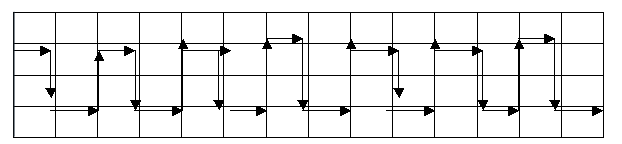
Laura S and Eleanor point out that "there are variations on this, which are just as long". Oliver says that he worked this out using
(PxL)-(P-2)
Perhaps you'd like to look into these patterns further.
You may also like
Geoboards
This practical challenge invites you to investigate the different squares you can make on a square geoboard or pegboard.