Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Six to Four
Age 5 to 7
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Six to Four
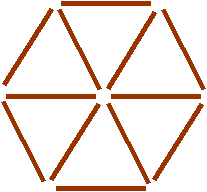
Move four sticks so there are exactly four triangles.
Why do this problem?
The problem as written could be offered as a quick starter activity, perhaps at the beginning of the day as the children come into class. However by introducing associated activities it can provide a rich context for mathematical talk and mathematical thinking.Possible approach
If you have an IWB you might choose to draw up 12 moveable thick lines to represent matches. If not an OHP with spent matches would work well.Make the hexagonal pattern as in the problem and ask the children how may matches there are, and what shapes they can see. How many of each shape can they see? Ask them to visualise what happens if they take just one match away. Ask how many matches there are now, and what shapes they can see. Did they visualise correctly? Did it matter which match they chose?
Give each pair of children twelve spent matches or equivalent to make their own model. Ask them to visualise what happens if they take two matches away, and then to do it. Again ask how many matches there are now, and what shapes they can see. Did it matter which matches they chose?
Do the same again, this time taking away three matches. Again ask what shapes, how many, and whether it matters which matches they take. Draw attention to the possible different sizes of triangles and how many matches are needed for each.
Then pose the problem and allow some time for the children to have a go. Point out that although they are taking away matches as before, this time they are replacing them.
After some time bring the class together to share their solutions and talk about how they did it. Listen for explanations that use ideas from the previous discussion.
Key questions
How many triangles are we trying to make?What is the most number of matches we would need?
Possible extension
Using isometric paper, children can make up their own puzzles and record the solution with ordered pictures, making a 'film strip' of which matches they moved to where. They then show them to a partner and see if they can follow the instructions. (They could also compare which
instructions are better, words or pictures.)
There is a collection of similar style problems here.