Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Intersecting Squares
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
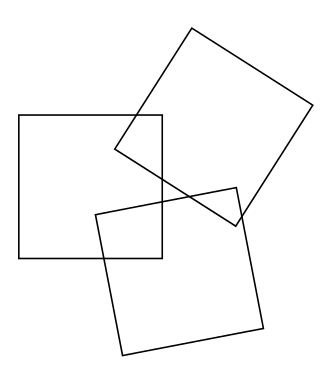
Three congruent squares overlap as shown.
The areas of the three overlapping sections are $2\;\mathrm{cm}^2$, $5\;\mathrm{cm}^2$ and $8\;\mathrm{cm}^2$ respectively.
The total area of the non-overlapping parts of the squares is $117\;\mathrm{cm}^2$.
What is the side length of each square?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Consecutive Numbers
An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.
Days and Dates
Investigate how you can work out what day of the week your birthday will be on next year, and the year after...