Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
One or Two
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
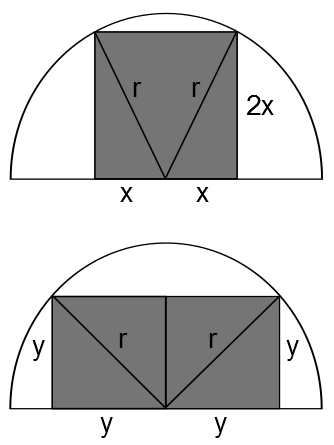
Let the radius of each semicircle be $r$.
In the top diagram, let the side-length of the square be $2x$. By Pythagoras' Theorem,
$x^2 + (2x)^2 = r^2$ and so $5x^2 = r^2$. So this shaded area is $(2x)^2 = 4x^2 = \frac{4r^2}{5}$.
In the bottom diagram, let the side-length of each square be $y$. Then by Pythagoras' Theorem, $y^2 + y^2 = r^2$ and so $2y^2 = r^2$. So this shaded area is $r^2$.
Therefore the ratio of the two shaded areas is $\frac{4}{5} : 1 = 4 : 5$.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
Bendy Quad
Four rods are hinged at their ends to form a convex quadrilateral. Investigate the different shapes that the quadrilateral can take. Be patient this problem may be slow to load.