Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Triangular Teaser
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
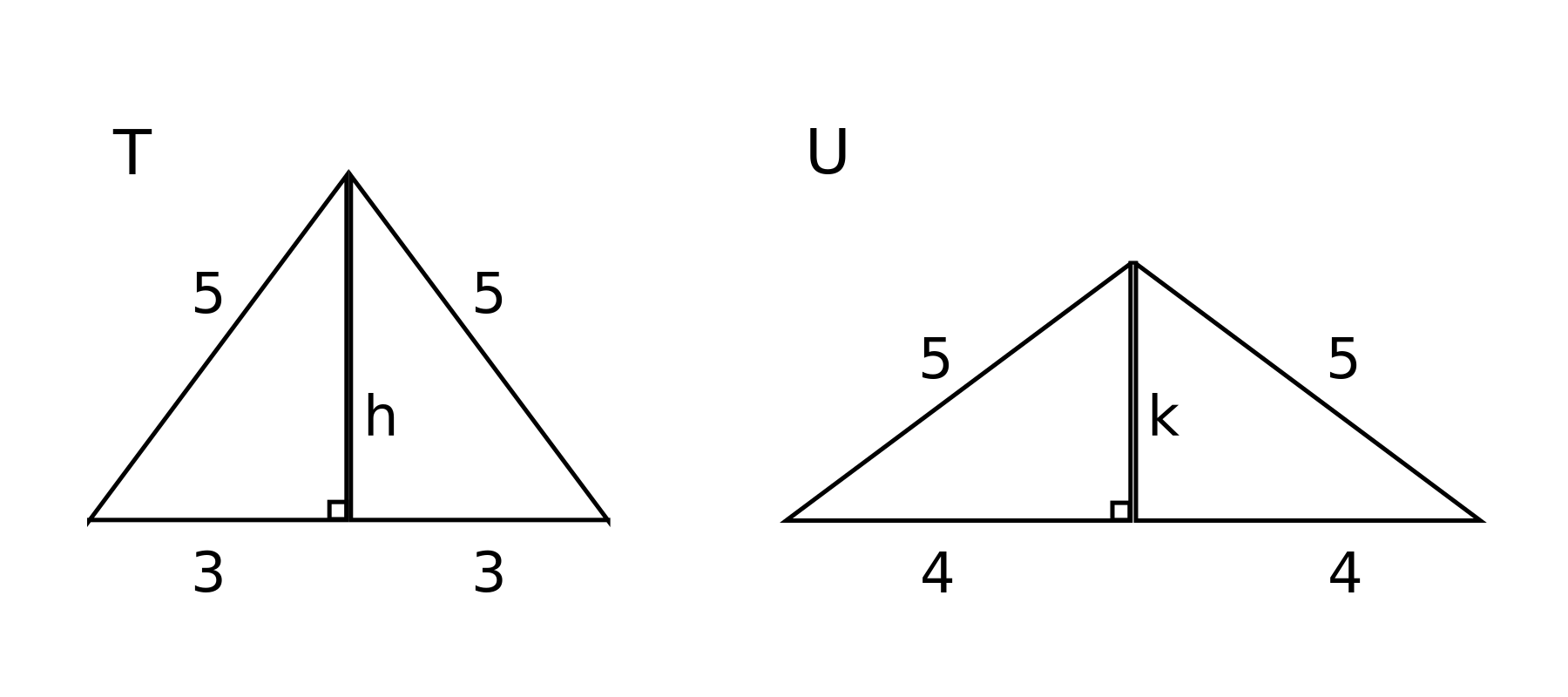
The diagram below shows isosceles triangles $T$ and $U$. The perpendicular from the top vertex to the base divides an isosceles triangle into two congruent right-angled triangles as shown in both $T$ and $U$. Evidently, by Pythagoras' Theorem, $h = 4$ and $k = 3$. So both triangles $T$ and $U$ consist of two $3$, $4$, $5$ triangles and therefore have equal areas.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.