Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Tadpoles
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
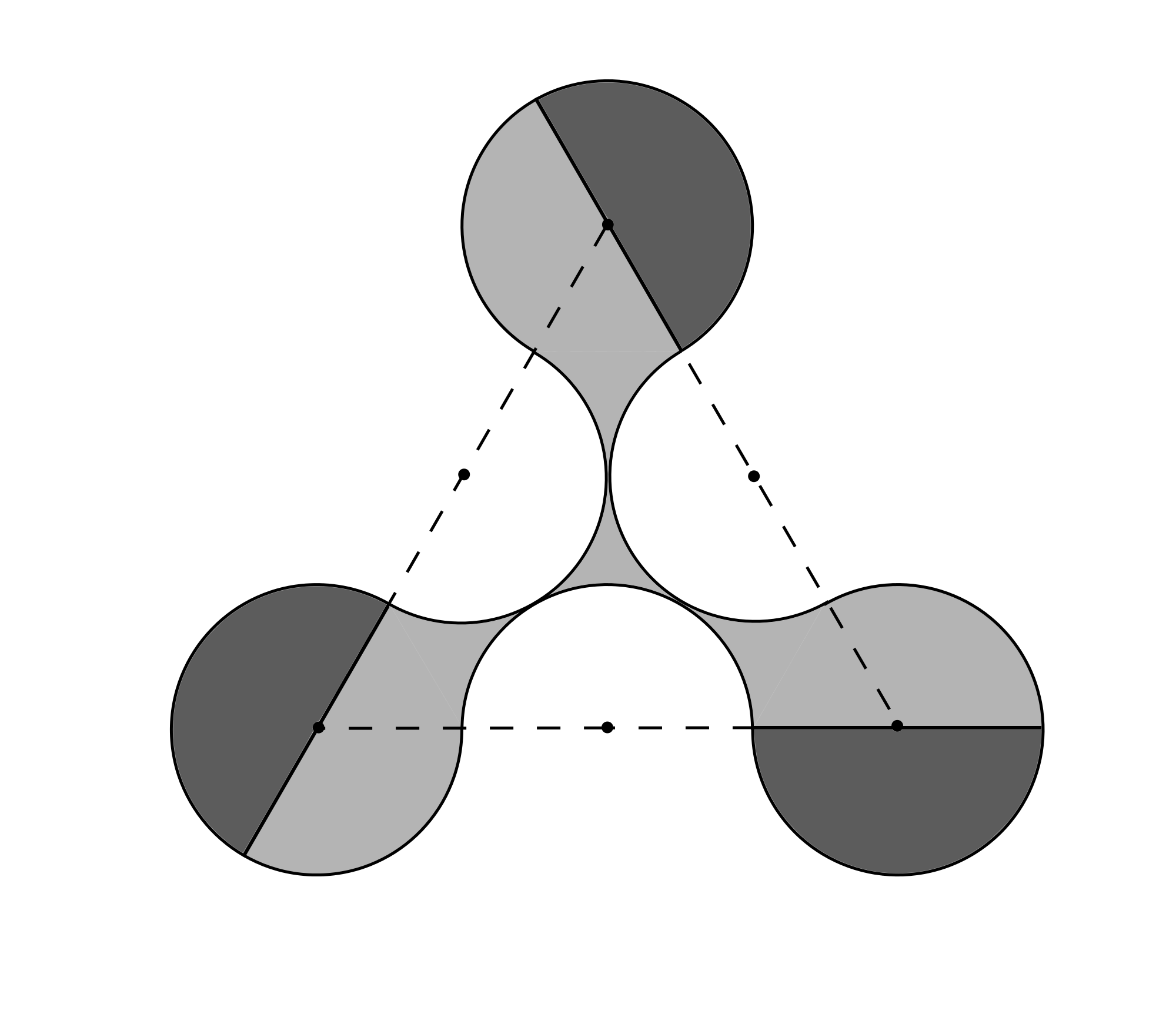
Before you read through the full solution, have a look at the following diagram.
Can you see how one might use it in the solution?
Click the "Show Hidden Text" Button to see the full solution.
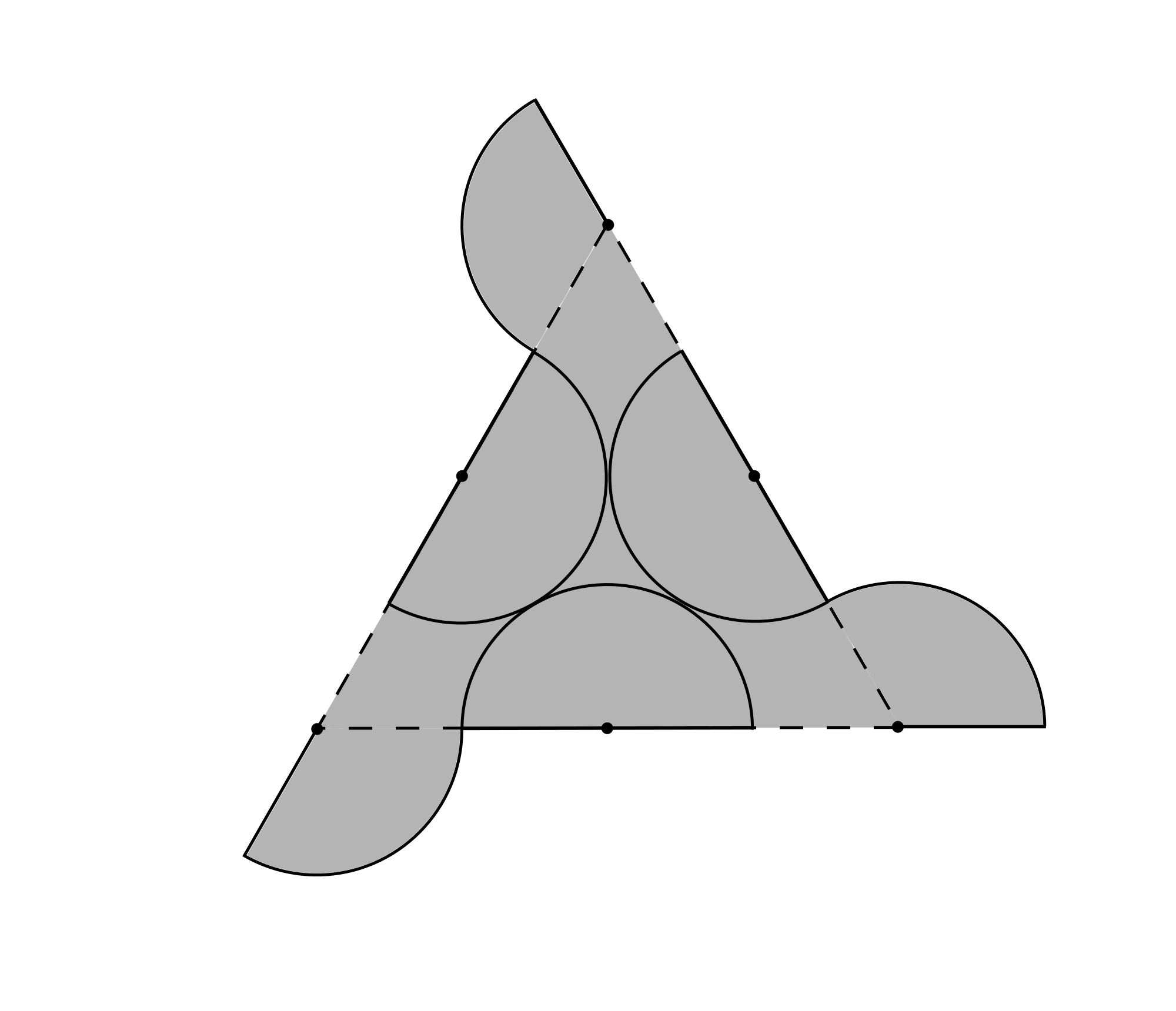
The length of the side of the triangle is equal to four times the radius of the arcs. So the arcs have radius $2\div 4 = \frac{1}{2}.$ In the diagram above, three semicircles have been shaded dark grey. The second diagram shows how these semicircles may be placed inside the triangle so that the whole triangle is shaded.
Therefore, the difference between the area of the shaded shape and the area of the triangle is the sum of the areas of three sectors of a circle. The interior angle of an equilateral triangle is $60^\circ$, so the angle at the centre of each sector is $180^\circ-60^\circ=120^\circ.$
Therefore, each sector is equal in area to one-third of the area of a circle. Their combined area is equal to the area of a circle of radius $\frac{1}{2}.$ So the required area is $\pi\times\left(\frac{1}{2}\right)^2 = \frac{\pi}{4}.$
Therefore, the difference between the area of the shaded shape and the area of the triangle is the sum of the areas of three sectors of a circle. The interior angle of an equilateral triangle is $60^\circ$, so the angle at the centre of each sector is $180^\circ-60^\circ=120^\circ.$
Therefore, each sector is equal in area to one-third of the area of a circle. Their combined area is equal to the area of a circle of radius $\frac{1}{2}.$ So the required area is $\pi\times\left(\frac{1}{2}\right)^2 = \frac{\pi}{4}.$

This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.