 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
First Connect Three for Two



- Game
Here's a game to play with an adult!
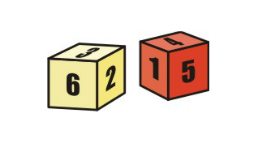
How do you play?
You'll need an adult to play with.
You'll also need a board to play on, two 1-6 dice, and counters in two different colours. Alternatively, you could use the interactive version below (scroll down a little).
In this game the winner is the first to complete a row of three, either horizontally, vertically or diagonally.
Roll the dice, place each dice in one of the squares and decide whether you want to add or subtract to produce a total shown on the board. Your total will then be covered with a counter.
You cannot cover a number which has already been covered.
If you are unable to find a total which has not been covered you must Pass.
Are there some numbers that you should be aiming for? Why?
Which number on the grid is the easiest to get? Why?
Which number is the most difficult to get? Why?
This problem is a great way for children to take responsibility for their own learning. They can avoid negative numbers if they are not confident or they can push themselves to calculate negative answers. In analysing the game more fully, rather than just playing it, the idea is for children to develop a system for finding all the possible ways of making each number on the grid so they can justify which are the easiest to get.
Easier version: try changing the board so that only the numbers $1$-$12$ are included.
Harder version: try changing the shape of the board, or change the game so that some numbers appear more than once on the board and you can place more than one counter in a turn. You could also try and design a board for a game where multiplication and division are allowed.
Repeat the game, aiming to find a winning strategy, then talk together about how it was found.
There's a classroom version of this game here.