Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Wag Worms
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Wag Worms
When intergalactic Wag Worms are born they look just like a cube.

Each year they grow another cube in any direction (except on their faces of course). So a Wag Worm in its second year might look like any of these.
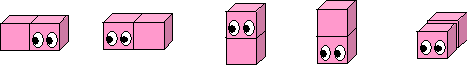
The next year it grows another cube onto its second cube (not its face cube). So one shape a Worm in its third year can be is this:

Find all the shapes that a Wag Worm in its third year can be.
Why do this problem?
This activity gives you a good opportunity to encourage pupils to make sense of, and interpret, situations. It also gives them a chance to share ways of convincing you they have found all the possibilities, which is quite a challenge in this problem.
Possible approach
It would be good to introduce the problem using some interlocking cubes. Draw a face on the face of one cube, or stick a sticker on a face, and explain to the group that this is what the Wag Worms look like when they are born. Continue by telling the children that each year, they grow one more cube. You could show one example and then ask some children to make other two-year old Wag Worms so
that you have all the possibilities. Encourage children to explain how they know they have got them all - each Worm has the second cube on a different face and there are five faces that this second cube could go on so there are five possibilities.
Ask them to guess what three-year-old Wag Worms look like and after clarifying the 'rules', set them off to try to find all the worms in pairs. Having a large supply of cubes will help and if you have enough, you'll be able to let the children keep a model of each worm rather than asking them to record their work, which might be quite tricky. If cubes are in short supply, you could make a
class set of all the Worms, so designate a particular table to collecting them. Of course you could take photos as well.
Bring the children together to talk about how they have gone about finding the Worms. Invite those children who had some sort of system to explain what it was so everyone could replicate that particular way. For example, one way would be to start with the first two-year old Worm and look at all the different possible places to put a third cube, then to look at a second two-year-old Worm and
do the same thing etc. If the children have struggled to use a system at all, you could ask them to look at the Worms they've made and sort them into groups. This might help them notice ones they have missed out.
Key questions
How did you find these?
Do you have a system (method, idea, recipe) for getting more solutions?
Possible extension
Encourage the pupils to ask, "I wonder what would happen if I ...?". For example, they could go on to look at four cubes. In this case, they may need to consider what to do when they want to add a further cube but this cube would cover the Worm's face even though it is not connected to it:
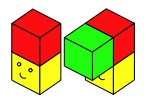
Would it be okay to add another cube on the underneath side of the green?
Possible support
You could suggest that children start with one of the two-year-old Worms and find all the possible ways of adding one cube.