A version of this article first appeared in Equals, a journal published online by the Mathematical Assocation, which can be found here.

This article shows how a few interlocking cubes can help focus:

pupils' attention on:
• working systematically
• choosing effective recording methods
• making generalisations

and teachers' attention on:
• sharing ideas
• precision of arguments.

All that is needed is a large supply of interlocking cubes, for example Multilink.

Different towers

 

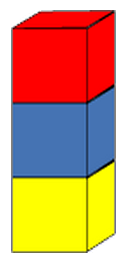
3 Blocks Towers offers a simple starting point, inviting learners to use three differently-coloured cubes to create as many towers as possible. There are two parts to this problem - firstly making as many different towers as you can think of and then being sure that all possible ones have been made. The first is relatively straight-forward, the second requires some systematic working and logical thinking. Having discussed some ways of making sure all the combinations have been found, each pair can be given three different colours of blocks to replicate the activity and convince you that they have found all possible towers.

All the possibilities?

 

Two on Five also requires systematic working. This time, seven cubes - five of them of one colour and two of another - are joined according to these rules:
• The five that are of one colour must all touch the table that you are working on;
• The two that are of a different colour must not touch the table.

Again, the challenge is to find all the possibilities.
Not only does this give pupils the chance to produce their own system for exploration, it gives a wonderful opportunity for them to explore ways of recording.

Why not?

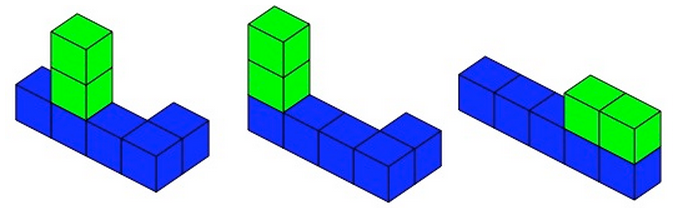
Brush Loads begins with just five cubes joined so that they don't topple over. Children are challenged to find out how many 'brush loads' of paint (one 'brush load' is enough for one square face) will be needed to cover the cubes, assuming that the base which touches the table is not painted. What is the least number of brush loads a five-cube model may need? The most? Learners are invited to investigate larger numbers of cubes. Can they make conjectures about how to arrange the cubes to get the least and the most number of brush loads? Can they explain their thinking?

Leading on to:

 

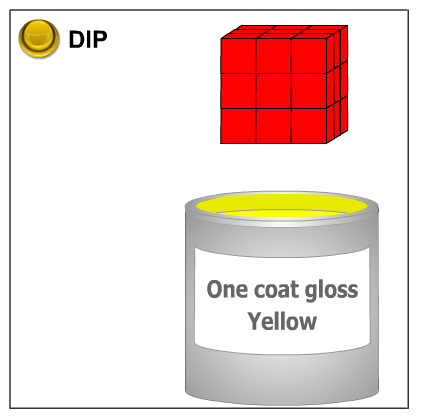
Painted Cube, where students are asked to imagine a large cube made up from 27 small red cubes. The large cube is dipped into a pot of yellow paint so the whole outer surface is covered, and then broken up into small cubes.

How many of the small cubes will have yellow paint on their faces? Will they all look the same?

Imagine doing the same thing with the other cubes made up from small red cubes.
What can you say about the number of small cubes with yellow paint on?

Exploring a variety of painted cubes may produce patterns, which learners can describe spatially, numerically and algebraically. They can appreciate the benefits of keeping a clear record of results, and apply their insights from the first case to ask themselves questions about further cases. This problem lends itself to collaborative working, both for students who are inexperienced at working in a group and those who are used to working in this way.

Going a little further:

Castles in the Middle is one of a series of activities which encourages the development of team-building skills such as listening, finding out what others think, giving reasons for ideas and pulling ideas together.